funkcja
mat. jedno z centralnych pojęć całej matematyki, w szczególności analizy matematycznej, ale także innych działów, m.in. topologii i teorii mnogości;
[łac. functio ‘czynność’],
odwzorowanie, przekształcenie,
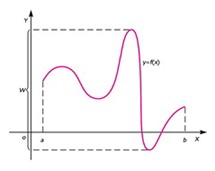
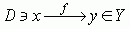 lub krócej y = f(x); element x nazywa się zmienną niezależną lub argumentem funkcji, a element y — wartością funkcji lub niekiedy (nieściśle) zmienną zależną (od x); zbiór D nazywa się zbiorem argumentów lub dziedziną funkcji; zbiór tych elementów y ∈ Y, które są wartościami rozważanej funkcji, tworzy tzw. zbiór W wartości funkcji lub jej przeciwdziedzinę (W jest na ogół częścią zbioru Y); gdy W = Y mówi się o funkcji „na” (funkcja ze zbioru D na Y). Funkcjami są np. ciągi, operacje, operatory, działania. Jeśli w szczególności elementy x są układami liczb: x1, x2, ... , xn, a zbiór Y jest zbiorem liczb rzeczywistych, to wtedy o funkcji y = f(x1, x2, ... , xn) mówi się jako o funkcji wielu zmiennych. Wykresem funkcji y = f(x) nazywa się podzbiór iloczynu (produktu) kartezjańskiego D × W, składający się z par postaci (x, f(x)), gdzie x ∈ D, f(x) = y ∈W. W najprostszym przypadku, kiedy zarówno x, jak i y są liczbami, funkcję y = f(x) na ogół można wykreślić w prostokątnym układzie współrzędnych kartezjańskich; gdy w szczególności funkcja jest ciągła, jej wykres przedstawia linię ciągłą (bez przerw). Często też funkcja jest zadawana za pomocą tabelki (zwłaszcza w naukach empirycznych). Funkcje mogą mieć rozmaite własności, np. mogą być stałe (postaci f(x) = c, gdzie c — stała), ograniczone (zbiór wartości funkcji W jest ograniczony), ciągłe, różniczkowalne, monotoniczne, różnowartościowe. Po raz pierwszy terminu funkcja użył 1692 G.W. Leibniz; pierwsze określenie funkcji bliskie podanemu wyżej dał 1718 Johann Bernoulli. Nowoczesne pojęcie funkcji przypisuje się P.G. Dirichletowi (1837).
lub krócej y = f(x); element x nazywa się zmienną niezależną lub argumentem funkcji, a element y — wartością funkcji lub niekiedy (nieściśle) zmienną zależną (od x); zbiór D nazywa się zbiorem argumentów lub dziedziną funkcji; zbiór tych elementów y ∈ Y, które są wartościami rozważanej funkcji, tworzy tzw. zbiór W wartości funkcji lub jej przeciwdziedzinę (W jest na ogół częścią zbioru Y); gdy W = Y mówi się o funkcji „na” (funkcja ze zbioru D na Y). Funkcjami są np. ciągi, operacje, operatory, działania. Jeśli w szczególności elementy x są układami liczb: x1, x2, ... , xn, a zbiór Y jest zbiorem liczb rzeczywistych, to wtedy o funkcji y = f(x1, x2, ... , xn) mówi się jako o funkcji wielu zmiennych. Wykresem funkcji y = f(x) nazywa się podzbiór iloczynu (produktu) kartezjańskiego D × W, składający się z par postaci (x, f(x)), gdzie x ∈ D, f(x) = y ∈W. W najprostszym przypadku, kiedy zarówno x, jak i y są liczbami, funkcję y = f(x) na ogół można wykreślić w prostokątnym układzie współrzędnych kartezjańskich; gdy w szczególności funkcja jest ciągła, jej wykres przedstawia linię ciągłą (bez przerw). Często też funkcja jest zadawana za pomocą tabelki (zwłaszcza w naukach empirycznych). Funkcje mogą mieć rozmaite własności, np. mogą być stałe (postaci f(x) = c, gdzie c — stała), ograniczone (zbiór wartości funkcji W jest ograniczony), ciągłe, różniczkowalne, monotoniczne, różnowartościowe. Po raz pierwszy terminu funkcja użył 1692 G.W. Leibniz; pierwsze określenie funkcji bliskie podanemu wyżej dał 1718 Johann Bernoulli. Nowoczesne pojęcie funkcji przypisuje się P.G. Dirichletowi (1837).