całka,
mat. jedno z podstawowych pojęć matematyki, wprowadzone niezależnie przez I. Newtona i G.W. Leibniza pod koniec XVII w. jako nowe narzędzie rachunkowe;
całka
Encyklopedia PWN
ma szerokie zastosowania nie tylko w matematyce, ale i w dziedzinach z nią związanych, głównie w fizyce i technice (pierwotnie miała służyć jako narzędzie do obliczania pól i objętości figur geometrycznych). Występuje w dwóch podstawowych, ściśle ze sobą związanych, znaczeniach: całki nieoznaczonej i całki oznaczonej.
Całka nieoznaczona. Funkcją pierwotną funkcji f(x) w określonym przedziale nazywa się każdą funkcję F(x), której pochodna F'(x) jest równa funkcji f(x) w każdym punkcie tego przedziału: F'(x) = f(x). Funkcje postaci F(x) + C (C — dowolnie ustalona liczba) — i tylko takie — są również funkcjami pierwotnymi funkcji f(x). Wyrażenie F(x) + C nazywa się całką nieoznaczoną i oznacza symbolem ∫ f(x)dx (f(x) — funkcja podcałkowa). Każda funkcja ciągła ma całkę nieoznaczoną (niektóre nieciągłe również), chociaż wiele z nich trudno się oblicza. Nie każdą całkę nieoznaczoną można wyrazić za pomocą funkcji elementarnych — przykładem mogą być całki 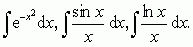
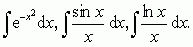
Całka oznaczona (według Riemanna). Niech f(x) będzie funkcją ograniczoną, określoną w przedziale [a, b], tj. dla a ≤ x ≤ b. Wybrane punkty a = x0 < x1 < ... < xn = b dzielą przedział [a, b] na przedziały częściowe: [x0, x1], [x1, x2], ..., [xn − 1, xn] o długościach Δx1 = x1 − x0, ..., Δxi = xi − xi − 1, ..., Δxn = xn − xn − 1; największą spośród tych liczb nazywa się średnicą danego przedziału; w każdym z przedziałów częściowych [xi − 1, xi] wybiera się dowolnie liczbę ξi i tworzy sumę całkową Riemanna 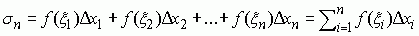 . Jeżeli dla każdego ciągu podziałów o średnicach dążących do zera (tzw. ciąg normalny podziałów) i każdego wyboru punktów ξi odpowiadające im sumy całkowe σn dążą do tej samej granicy, to granicę tę nazywa się całką oznaczoną Riemanna funkcji f(x) w przedziale [a, b] i oznacza symbolem
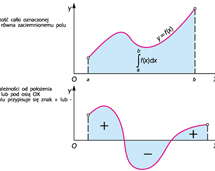
. Jeżeli dla każdego ciągu podziałów o średnicach dążących do zera (tzw. ciąg normalny podziałów) i każdego wyboru punktów ξi odpowiadające im sumy całkowe σn dążą do tej samej granicy, to granicę tę nazywa się całką oznaczoną Riemanna funkcji f(x) w przedziale [a, b] i oznacza symbolem 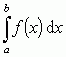 , przy czym a, b nazywa się granicami całkowania. Zarówno suma całkowa, jak i całka oznaczona mają określony sens geometryczny: suma całkowa jest równa polu zakreskowanej figury (suma pól prostokątów, które przy kolejnych podziałach będą coraz „cieńsze”), a całka oznaczona — polu ograniczonemu wykresem funkcji y = f(x), osią OX i pionowymi prostymi wystawionymi w punktach a i b; pole nad osią uważa się za dodatnie, pod osią — za ujemne.
, przy czym a, b nazywa się granicami całkowania. Zarówno suma całkowa, jak i całka oznaczona mają określony sens geometryczny: suma całkowa jest równa polu zakreskowanej figury (suma pól prostokątów, które przy kolejnych podziałach będą coraz „cieńsze”), a całka oznaczona — polu ograniczonemu wykresem funkcji y = f(x), osią OX i pionowymi prostymi wystawionymi w punktach a i b; pole nad osią uważa się za dodatnie, pod osią — za ujemne.
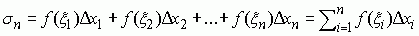 . Jeżeli dla każdego ciągu podziałów o średnicach dążących do zera (tzw. ciąg normalny podziałów) i każdego wyboru punktów ξi odpowiadające im sumy całkowe σn dążą do tej samej granicy, to granicę tę nazywa się całką oznaczoną Riemanna funkcji f(x) w przedziale [a, b] i oznacza symbolem
. Jeżeli dla każdego ciągu podziałów o średnicach dążących do zera (tzw. ciąg normalny podziałów) i każdego wyboru punktów ξi odpowiadające im sumy całkowe σn dążą do tej samej granicy, to granicę tę nazywa się całką oznaczoną Riemanna funkcji f(x) w przedziale [a, b] i oznacza symbolem 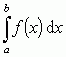 , przy czym a, b nazywa się granicami całkowania. Zarówno suma całkowa, jak i całka oznaczona mają określony sens geometryczny: suma całkowa jest równa polu zakreskowanej figury (suma pól prostokątów, które przy kolejnych podziałach będą coraz „cieńsze”), a całka oznaczona — polu ograniczonemu wykresem funkcji y = f(x), osią OX i pionowymi prostymi wystawionymi w punktach a i b; pole nad osią uważa się za dodatnie, pod osią — za ujemne.
, przy czym a, b nazywa się granicami całkowania. Zarówno suma całkowa, jak i całka oznaczona mają określony sens geometryczny: suma całkowa jest równa polu zakreskowanej figury (suma pól prostokątów, które przy kolejnych podziałach będą coraz „cieńsze”), a całka oznaczona — polu ograniczonemu wykresem funkcji y = f(x), osią OX i pionowymi prostymi wystawionymi w punktach a i b; pole nad osią uważa się za dodatnie, pod osią — za ujemne. Jeśli funkcja f(x) ma przedziale [a, b] całkę nieoznaczoną (funkcję pierwotną F(x)), to związek między nią a całką oznaczoną wyraża podstawowy wzór rachunku całkowego (wzór Leibniza–Newtona): 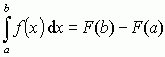 . Numeryczne obliczanie całek oznaczonych rzadko opiera się na tym wzorze, gdyż funkcje pierwotne wyrażają się w sposób elementarny tylko dla wąskiej klasy funkcji — w praktyce stosuje się różne metody przybliżone.
. Numeryczne obliczanie całek oznaczonych rzadko opiera się na tym wzorze, gdyż funkcje pierwotne wyrażają się w sposób elementarny tylko dla wąskiej klasy funkcji — w praktyce stosuje się różne metody przybliżone.
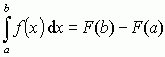 . Numeryczne obliczanie całek oznaczonych rzadko opiera się na tym wzorze, gdyż funkcje pierwotne wyrażają się w sposób elementarny tylko dla wąskiej klasy funkcji — w praktyce stosuje się różne metody przybliżone.
. Numeryczne obliczanie całek oznaczonych rzadko opiera się na tym wzorze, gdyż funkcje pierwotne wyrażają się w sposób elementarny tylko dla wąskiej klasy funkcji — w praktyce stosuje się różne metody przybliżone. Termin całka występuje również z innymi określeniami, m.in.: całka niewłaściwa — pojęcie definiowane jako graniczna wartość całki oznaczonej w przypadku nieskończonych granic całkowania (np. 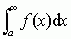 ) lub też nieograniczonej funkcji podcałkowej; całka wielokrotna — całka oznaczona funkcji n zmiennych, w której całkowanie odbywa się po przestrzeni n-wymiarowej, np. całkę podwójną (dwukrotną) definiuje się dla funkcji f(x, y) określonej w ograniczonym obszarze Δ, stosuje się podział tego obszaru na kwadraciki, wybiera w każdym punkt (ξi, ηi), tworzy sumy całkowe analogicznie jak w pojedynczej całce oznaczonej i jak tam — definiuje się całkę jako granicę tych sum; oznaczana
) lub też nieograniczonej funkcji podcałkowej; całka wielokrotna — całka oznaczona funkcji n zmiennych, w której całkowanie odbywa się po przestrzeni n-wymiarowej, np. całkę podwójną (dwukrotną) definiuje się dla funkcji f(x, y) określonej w ograniczonym obszarze Δ, stosuje się podział tego obszaru na kwadraciki, wybiera w każdym punkt (ξi, ηi), tworzy sumy całkowe analogicznie jak w pojedynczej całce oznaczonej i jak tam — definiuje się całkę jako granicę tych sum; oznaczana 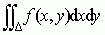 ; geometrycznie całkę podwójną interpretuje się jako objętość obszaru pod wykresem funkcji f(x, y); całka iterowana — wygodna do rachunków postać całki wielokrotnej, w której kolejno powtarza się całkowanie jednokrotne względem poszczególnych zmiennych (pozostałe zmienne traktując w danej chwili jako parametry), oznaczana
; geometrycznie całkę podwójną interpretuje się jako objętość obszaru pod wykresem funkcji f(x, y); całka iterowana — wygodna do rachunków postać całki wielokrotnej, w której kolejno powtarza się całkowanie jednokrotne względem poszczególnych zmiennych (pozostałe zmienne traktując w danej chwili jako parametry), oznaczana 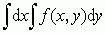 ; całka krzywoliniowa, np.
; całka krzywoliniowa, np. 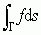 , w której całkowanie wykonuje się po zadanym łuku krzywej Γ, stosowana np. do obliczania pracy; całka powierzchniowa, np. ∫S fds — całkowanie wykonuje się po płacie S określonej powierzchni; za jej pomocą oblicza się m.in. strumień pola wektorowego przez tę powierzchnię.
, w której całkowanie wykonuje się po zadanym łuku krzywej Γ, stosowana np. do obliczania pracy; całka powierzchniowa, np. ∫S fds — całkowanie wykonuje się po płacie S określonej powierzchni; za jej pomocą oblicza się m.in. strumień pola wektorowego przez tę powierzchnię.
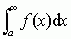 ) lub też nieograniczonej funkcji podcałkowej; całka wielokrotna — całka oznaczona funkcji n zmiennych, w której całkowanie odbywa się po przestrzeni n-wymiarowej, np. całkę podwójną (dwukrotną) definiuje się dla funkcji f(x, y) określonej w ograniczonym obszarze Δ, stosuje się podział tego obszaru na kwadraciki, wybiera w każdym punkt (ξi, ηi), tworzy sumy całkowe analogicznie jak w pojedynczej całce oznaczonej i jak tam — definiuje się całkę jako granicę tych sum; oznaczana
) lub też nieograniczonej funkcji podcałkowej; całka wielokrotna — całka oznaczona funkcji n zmiennych, w której całkowanie odbywa się po przestrzeni n-wymiarowej, np. całkę podwójną (dwukrotną) definiuje się dla funkcji f(x, y) określonej w ograniczonym obszarze Δ, stosuje się podział tego obszaru na kwadraciki, wybiera w każdym punkt (ξi, ηi), tworzy sumy całkowe analogicznie jak w pojedynczej całce oznaczonej i jak tam — definiuje się całkę jako granicę tych sum; oznaczana 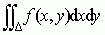 ; geometrycznie całkę podwójną interpretuje się jako objętość obszaru pod wykresem funkcji f(x, y); całka iterowana — wygodna do rachunków postać całki wielokrotnej, w której kolejno powtarza się całkowanie jednokrotne względem poszczególnych zmiennych (pozostałe zmienne traktując w danej chwili jako parametry), oznaczana
; geometrycznie całkę podwójną interpretuje się jako objętość obszaru pod wykresem funkcji f(x, y); całka iterowana — wygodna do rachunków postać całki wielokrotnej, w której kolejno powtarza się całkowanie jednokrotne względem poszczególnych zmiennych (pozostałe zmienne traktując w danej chwili jako parametry), oznaczana 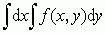 ; całka krzywoliniowa, np.
; całka krzywoliniowa, np. 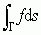 , w której całkowanie wykonuje się po zadanym łuku krzywej Γ, stosowana np. do obliczania pracy; całka powierzchniowa, np. ∫S fds — całkowanie wykonuje się po płacie S określonej powierzchni; za jej pomocą oblicza się m.in. strumień pola wektorowego przez tę powierzchnię.
, w której całkowanie wykonuje się po zadanym łuku krzywej Γ, stosowana np. do obliczania pracy; całka powierzchniowa, np. ∫S fds — całkowanie wykonuje się po płacie S określonej powierzchni; za jej pomocą oblicza się m.in. strumień pola wektorowego przez tę powierzchnię. Prapoczątki całki znajdujemy już w starożytności; metoda wyczerpywania, zwana też całkowaniem starożytnych lub całką Eudoksosa (Eudoksos z Knidos), polegała na mierzeniu pól i objętości figur przez przybliżanie ich ciągami figur o znanych miarach (najczęściej wielokątami i wielościanami); metodę tę stosował z powodzeniem Archimedes, który również obliczał objętości brył obrotowych dzieląc je na coraz cieńsze „plasterki”. Idee te zostały podjęte dopiero w końcu XVI w., np. Galileusz zauważył równoważność zagadnień: obliczania drogi w ruchu o zmiennej prędkości i obliczania pola figury o zmiennej wysokości. Zbliżonymi koncepcjami zajmowali się m.in. J. Kepler, B. Cavalieri, P. Fermat, B. Pascal, J. Wallis, I. Barrow. Syntezą powstałych w tym czasie konstrukcji było pojęcie całki, wprowadzone pod koniec XVII w. niezależnie przez Newtona i Leibniza. Ich drogi do tego pojęcia były różne, inaczej też rozłożyli w swoich teoriach akcenty. Newton położył większy nacisk na całkę nieoznaczoną (całkowanie jako działanie odwrotne do różniczkowania), Leibniz zaś — na całkę oznaczoną (całkowanie jako sumowanie „nieskończenie małych ” elementów f(x)dx). Rachunek różniczkowy i całkowy był tworzony w dużej mierze intuicyjnie, posługiwano się przy tym niejasnymi pojęciami i argumentacją (brak precyzyjnych definicji). Mimo to nastąpił jego bujny rozwój (m.in. Jakob i Johann Bernoulli, L. Euler) — od razu też stał się niezwykle skutecznym i uniwersalnym narzędziem rachunkowym matematyki i fizyki. Uściślenie stosowanych w nim pojęć nastąpiło dopiero w XIX w. dzięki pracom A. Cauchy’ego (pojęcie granicy, pojęcie funkcji ciągłej). Poprawną definicję całki ciągłej podał 1854 B. Riemann. Dalszy rozwój pojęcia całki jest związany z uogólnianiem go na szersze klasy funkcji, przy czym najważniejszym z tych uogólnień jest całka Lebesgue’a, podana 1902 przez H. Lebesgue’a, oparta na rozwiniętej przez niego teorii miary.
Polski termin „całka” zaproponowany przez Jana Śniadeckiego, jest odpowiednikiem terminu integral (łac. integer „całkowity”), używanego w wielu językach, a wprowadzonego przez Johanna Bernoulliego. Symbol całki jak większość oznaczeń rachunku różniczkowego i całkowego, pochodzi od Leibniza (stylizowana litera S — pierwsza w łacińskim wyrazie summa).