Gaussa–Ostrogradskiego wzór,
mat. wzór pozwala-jący zamieniać całkę powierzchniową zorientowaną na całkę potrójną i odwrotnie (całka);
Gaussa–Ostrogradskiego wzór
Encyklopedia PWN
ma postać:
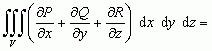
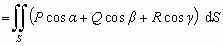
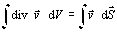
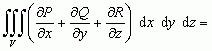
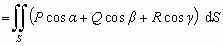
gdzie funkcje P(x, y, z), Q(x, y, z), R(x, y, z) są ciągłe wraz z pochodnymi ∂P/∂x, ∂Q/∂y, ∂R/∂z wewnątrz i na brzegu obszaru V, normalnego ze względu na 3 płaszczyzny współrz., przy czym brzeg S obszaru V jest kawałkami gładki, a cosα, cosβ, cosγ są odpowiednimi składowymi wektora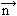 
wewnętrznej normalnej do powierzchni S. Wzór Gaussa–Ostrogradskiego udowodnił M. Ostrogradski (1828 i 1838); wcześniej C.F. Gauss zawarł go implicite w pracach z 1813 i 1830. W postaci wektorowej wzór Gaussa–Ostrogradskiego wygląda następująco:
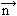wewnętrznej normalnej do powierzchni S. Wzór Gaussa–Ostrogradskiego udowodnił M. Ostrogradski (1828 i 1838); wcześniej C.F. Gauss zawarł go implicite w pracach z 1813 i 1830. W postaci wektorowej wzór Gaussa–Ostrogradskiego wygląda następująco: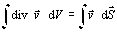 gdzie div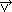 
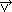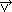— dywergencja pola , a d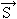
— iloczyn skalarny wektora 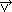przez skierowany element powierzchniowy d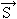. Wyrażenie 
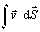nazywa się strumieniem pola 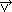przez powierzchnię S. Stosując w.G.–O. można przejść od różniczkowej do całkowej postaci prawa Gaussa.
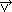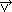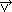— dywergencja pola , a d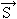 — iloczyn skalarny wektora 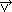przez skierowany element powierzchniowy d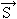. Wyrażenie 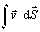nazywa się strumieniem pola 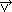przez powierzchnię S. Stosując w.G.–O. można przejść od różniczkowej do całkowej postaci prawa Gaussa.