miary teoria,
dział analizy mat., poświęcony abstrakcyjnym uogólnieniom znanych pojęć geometrii klas. i matematyki elementarnej: długości odcinka, pola wielokąta, objętości wielościanu, 0-wymiarowej miary liczącej, tzn. liczby elementów zbioru.
miary teoria
Encyklopedia PWN
Jednocześnie z rozwojem matematyki i dyscyplin pokrewnych pojawiła się potrzeba przypisywania miary obiektom bardziej skomplikowanym, np. całkę 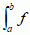 z funkcji dodatniej f definiuje się jako pole pod jej wykresem.
z funkcji dodatniej f definiuje się jako pole pod jej wykresem.
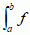 z funkcji dodatniej f definiuje się jako pole pod jej wykresem.
z funkcji dodatniej f definiuje się jako pole pod jej wykresem. Pierwsza ścisła definicja pojęcia miary i towarzyszącego mu pojęcia całki, uogólniająca klas. pojęcia, została podana 1851 przez B. Riemanna: 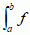 równa się granicy
równa się granicy 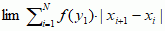 , gdzie punkty a = x1 < x2 < ... < xN + 1 = b tworzą rozbicie odcinka [a, b] na pododcinki Δi = [xi, xi + 1], zawierające punkty yi, tak że maks. długość pododcinków dąży do zera. Uważa się, że f jest całkowalna w sensie Riemanna, o ile powyższa granica istnieje i nie zależy od wyboru podziałów i punktów yi. Całka Riemanna jest dobrze określona dla funkcji ciągłych i kawałkami ciągłych (H. Lebesgue wykazał, że funkcja jest całkowalna w sensie Riemanna wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma zerową miarę Lebesgue’a). Miara Riemanna podzbioru A prostej rzeczywistej ℝ1 jest to całka Riemanna funkcji charakterystycznej zbioru,
, gdzie punkty a = x1 < x2 < ... < xN + 1 = b tworzą rozbicie odcinka [a, b] na pododcinki Δi = [xi, xi + 1], zawierające punkty yi, tak że maks. długość pododcinków dąży do zera. Uważa się, że f jest całkowalna w sensie Riemanna, o ile powyższa granica istnieje i nie zależy od wyboru podziałów i punktów yi. Całka Riemanna jest dobrze określona dla funkcji ciągłych i kawałkami ciągłych (H. Lebesgue wykazał, że funkcja jest całkowalna w sensie Riemanna wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma zerową miarę Lebesgue’a). Miara Riemanna podzbioru A prostej rzeczywistej ℝ1 jest to całka Riemanna funkcji charakterystycznej zbioru, 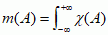 . O zbiorach, których funkcje charakterystyczne są całkowalne w sensie Riemanna, mówi się, że są mierzalne w sensie Riemanna. Definicja całki Riemanna funkcji f określonej na kostce G = [a1, b1] × ... × [an, bn] w przestrzeni euklidesowej ℝn jest analogiczna jak w przypadku ℝ1:
. O zbiorach, których funkcje charakterystyczne są całkowalne w sensie Riemanna, mówi się, że są mierzalne w sensie Riemanna. Definicja całki Riemanna funkcji f określonej na kostce G = [a1, b1] × ... × [an, bn] w przestrzeni euklidesowej ℝn jest analogiczna jak w przypadku ℝ1: 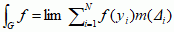 , gdzie Δi są n-wymiarowymi kostkami (o n-wymiarowych objętościach m(Δi)), zawierającymi punkty yi i tworzącymi rozbicie zbioru G. Przy tym średnica kostek dąży do zera, diam(Δi) < ε → 0. Podobnie dla podzbioru A ⊂ G jego miara Riemanna jest równa ∫GχA.
, gdzie Δi są n-wymiarowymi kostkami (o n-wymiarowych objętościach m(Δi)), zawierającymi punkty yi i tworzącymi rozbicie zbioru G. Przy tym średnica kostek dąży do zera, diam(Δi) < ε → 0. Podobnie dla podzbioru A ⊂ G jego miara Riemanna jest równa ∫GχA.
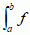 równa się granicy
równa się granicy 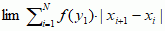 , gdzie punkty a = x1 < x2 < ... < xN + 1 = b tworzą rozbicie odcinka [a, b] na pododcinki Δi = [xi, xi + 1], zawierające punkty yi, tak że maks. długość pododcinków dąży do zera. Uważa się, że f jest całkowalna w sensie Riemanna, o ile powyższa granica istnieje i nie zależy od wyboru podziałów i punktów yi. Całka Riemanna jest dobrze określona dla funkcji ciągłych i kawałkami ciągłych (H. Lebesgue wykazał, że funkcja jest całkowalna w sensie Riemanna wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma zerową miarę Lebesgue’a). Miara Riemanna podzbioru A prostej rzeczywistej ℝ1 jest to całka Riemanna funkcji charakterystycznej zbioru,
, gdzie punkty a = x1 < x2 < ... < xN + 1 = b tworzą rozbicie odcinka [a, b] na pododcinki Δi = [xi, xi + 1], zawierające punkty yi, tak że maks. długość pododcinków dąży do zera. Uważa się, że f jest całkowalna w sensie Riemanna, o ile powyższa granica istnieje i nie zależy od wyboru podziałów i punktów yi. Całka Riemanna jest dobrze określona dla funkcji ciągłych i kawałkami ciągłych (H. Lebesgue wykazał, że funkcja jest całkowalna w sensie Riemanna wtedy i tylko wtedy, gdy zbiór jej punktów nieciągłości ma zerową miarę Lebesgue’a). Miara Riemanna podzbioru A prostej rzeczywistej ℝ1 jest to całka Riemanna funkcji charakterystycznej zbioru, 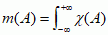 . O zbiorach, których funkcje charakterystyczne są całkowalne w sensie Riemanna, mówi się, że są mierzalne w sensie Riemanna. Definicja całki Riemanna funkcji f określonej na kostce G = [a1, b1] × ... × [an, bn] w przestrzeni euklidesowej ℝn jest analogiczna jak w przypadku ℝ1:
. O zbiorach, których funkcje charakterystyczne są całkowalne w sensie Riemanna, mówi się, że są mierzalne w sensie Riemanna. Definicja całki Riemanna funkcji f określonej na kostce G = [a1, b1] × ... × [an, bn] w przestrzeni euklidesowej ℝn jest analogiczna jak w przypadku ℝ1: 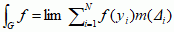 , gdzie Δi są n-wymiarowymi kostkami (o n-wymiarowych objętościach m(Δi)), zawierającymi punkty yi i tworzącymi rozbicie zbioru G. Przy tym średnica kostek dąży do zera, diam(Δi) < ε → 0. Podobnie dla podzbioru A ⊂ G jego miara Riemanna jest równa ∫GχA.
, gdzie Δi są n-wymiarowymi kostkami (o n-wymiarowych objętościach m(Δi)), zawierającymi punkty yi i tworzącymi rozbicie zbioru G. Przy tym średnica kostek dąży do zera, diam(Δi) < ε → 0. Podobnie dla podzbioru A ⊂ G jego miara Riemanna jest równa ∫GχA. Definicje miary i całki Riemanna są wygodne i powszechnie do dziś używane, jednak w pewnych przypadkach są niezadowalające. Okazało się np., że podzbiór punktów wymiernych odcinka [0, l] nie jest mierzalny w sensie Riemanna. Jest on przeliczalny, a zatem nieporównywalnie mniejszy od swojego uzupełnienia; tymczasem jego funkcja charakterystyczna jest nieciągła w każdym punkcie. Ostateczną definicję całki i miary w przestrzeniach euklidesowych podał Lebesgue (ok. 1900). Całka Lebesgue’a funkcji dodatniej f na przedziale [a, b] jest granicą 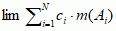 , gdzie punkty c1 < c2 < ... < cN+1 tworzą rozbicie zbioru wartości funkcji na pododcinki z maks. średnicą dążącą do zera oraz Ai = {x: ci ≤ f(x) < ci+1}. O zbiorach Ai zakłada się, że są mierzalne w sensie Lebesgue’a. Podzbiór A ⊂ [a, b] jest mierzalny w sensie Lebesgue’a, jeśli jego miara zewn. me(A) jest równa jego mierze wewn. mi(A) = |b − a| − me([a, b] \ A). Wtedy liczbę m(a) = me(A) = mi(A) nazywa się miarą Lebesgue’a zbioru A. Aby wyznaczyć miarę zewn., należy wziąć pokrycia zbioru A przeliczalnymi rodzinami odcinków o średnicach dążących do zera:
, gdzie punkty c1 < c2 < ... < cN+1 tworzą rozbicie zbioru wartości funkcji na pododcinki z maks. średnicą dążącą do zera oraz Ai = {x: ci ≤ f(x) < ci+1}. O zbiorach Ai zakłada się, że są mierzalne w sensie Lebesgue’a. Podzbiór A ⊂ [a, b] jest mierzalny w sensie Lebesgue’a, jeśli jego miara zewn. me(A) jest równa jego mierze wewn. mi(A) = |b − a| − me([a, b] \ A). Wtedy liczbę m(a) = me(A) = mi(A) nazywa się miarą Lebesgue’a zbioru A. Aby wyznaczyć miarę zewn., należy wziąć pokrycia zbioru A przeliczalnymi rodzinami odcinków o średnicach dążących do zera: 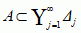 , diam(Δj) < ε → 0; wtedy granica dolna liczb
, diam(Δj) < ε → 0; wtedy granica dolna liczb 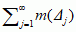 jest równa me(A). Funkcja f jest mierzalna w sensie Lebesgue’a, jeśli zbiory {x: f(x) < c} są mierzalne w sensie Lebesgue’a. Całka Lebesgue’a jest określona tylko dla funkcji mierzalnych w sensie Lebesgue’a (większość znanych funkcji, np. funkcja charakterystyczna zbioru punktów wymiernych odcinka [0, 1], ma tę własność). Zastąpienie odcinków Δi n-wymiarowymi kostkami umożliwia uogólnienie definicji całki Lebesgue’a na przypadek funkcji w ℝn.
jest równa me(A). Funkcja f jest mierzalna w sensie Lebesgue’a, jeśli zbiory {x: f(x) < c} są mierzalne w sensie Lebesgue’a. Całka Lebesgue’a jest określona tylko dla funkcji mierzalnych w sensie Lebesgue’a (większość znanych funkcji, np. funkcja charakterystyczna zbioru punktów wymiernych odcinka [0, 1], ma tę własność). Zastąpienie odcinków Δi n-wymiarowymi kostkami umożliwia uogólnienie definicji całki Lebesgue’a na przypadek funkcji w ℝn.
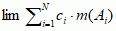 , gdzie punkty c1 < c2 < ... < cN+1 tworzą rozbicie zbioru wartości funkcji na pododcinki z maks. średnicą dążącą do zera oraz Ai = {x: ci ≤ f(x) < ci+1}. O zbiorach Ai zakłada się, że są mierzalne w sensie Lebesgue’a. Podzbiór A ⊂ [a, b] jest mierzalny w sensie Lebesgue’a, jeśli jego miara zewn. me(A) jest równa jego mierze wewn. mi(A) = |b − a| − me([a, b] \ A). Wtedy liczbę m(a) = me(A) = mi(A) nazywa się miarą Lebesgue’a zbioru A. Aby wyznaczyć miarę zewn., należy wziąć pokrycia zbioru A przeliczalnymi rodzinami odcinków o średnicach dążących do zera:
, gdzie punkty c1 < c2 < ... < cN+1 tworzą rozbicie zbioru wartości funkcji na pododcinki z maks. średnicą dążącą do zera oraz Ai = {x: ci ≤ f(x) < ci+1}. O zbiorach Ai zakłada się, że są mierzalne w sensie Lebesgue’a. Podzbiór A ⊂ [a, b] jest mierzalny w sensie Lebesgue’a, jeśli jego miara zewn. me(A) jest równa jego mierze wewn. mi(A) = |b − a| − me([a, b] \ A). Wtedy liczbę m(a) = me(A) = mi(A) nazywa się miarą Lebesgue’a zbioru A. Aby wyznaczyć miarę zewn., należy wziąć pokrycia zbioru A przeliczalnymi rodzinami odcinków o średnicach dążących do zera: 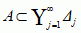 , diam(Δj) < ε → 0; wtedy granica dolna liczb
, diam(Δj) < ε → 0; wtedy granica dolna liczb 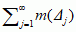 jest równa me(A). Funkcja f jest mierzalna w sensie Lebesgue’a, jeśli zbiory {x: f(x) < c} są mierzalne w sensie Lebesgue’a. Całka Lebesgue’a jest określona tylko dla funkcji mierzalnych w sensie Lebesgue’a (większość znanych funkcji, np. funkcja charakterystyczna zbioru punktów wymiernych odcinka [0, 1], ma tę własność). Zastąpienie odcinków Δi n-wymiarowymi kostkami umożliwia uogólnienie definicji całki Lebesgue’a na przypadek funkcji w ℝn.
jest równa me(A). Funkcja f jest mierzalna w sensie Lebesgue’a, jeśli zbiory {x: f(x) < c} są mierzalne w sensie Lebesgue’a. Całka Lebesgue’a jest określona tylko dla funkcji mierzalnych w sensie Lebesgue’a (większość znanych funkcji, np. funkcja charakterystyczna zbioru punktów wymiernych odcinka [0, 1], ma tę własność). Zastąpienie odcinków Δi n-wymiarowymi kostkami umożliwia uogólnienie definicji całki Lebesgue’a na przypadek funkcji w ℝn. Miara Lebesgue’a jest szczególnym przypadkiem miary przeliczalnie addytywnej. W klasie wszystkich podzbiorów ustalonego zbioru Ω jest wyróżniona klasa M podzbiorów o następujących własnościach: (1) Ω ∈ M, (2) jeśli A ∈ M, to X \ A ∈ M, (3) jeśli A1, A2, ... ∈ M, to 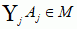 . Taka klasa nazywa się σ-algebrą (lub σ-ciałem). Przykładami są: σ-algebra podzbiorów ℝn mierzalnych w sensie Lebesgue’a i σ-algebra podzbiorów borelowskich (zbiór borelowski) przestrzeni metrycznej generowana przez podzbiory otwarte. Miarą przeliczalnie addytywną na M nazywa się funkcję m: M → ℝ o własności: jeśli A1, A2, ... ∈ M i Ai ∩ Aj = ∅, i ≠ j, to
. Taka klasa nazywa się σ-algebrą (lub σ-ciałem). Przykładami są: σ-algebra podzbiorów ℝn mierzalnych w sensie Lebesgue’a i σ-algebra podzbiorów borelowskich (zbiór borelowski) przestrzeni metrycznej generowana przez podzbiory otwarte. Miarą przeliczalnie addytywną na M nazywa się funkcję m: M → ℝ o własności: jeśli A1, A2, ... ∈ M i Ai ∩ Aj = ∅, i ≠ j, to 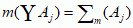 . Miara jest dodatnia, jeśli przyjmuje wartości dodatnie; jeśli dodatkowo m(Ω) = 1, wówczas jest to miara probabilistyczna. W matematyce i fizyce są badane też miary przyjmujące wartości w bardziej ogólnych przestrzeniach, np. miary spektralne. Podobnie jak przedstawiono wyżej, wprowadza się pojęcia funkcji f na Ω, mierzalnej względem σ-algebry M i jej całki względem miary m, ∫Ωfdm. Miara Lebesgue’a jest przykładem miary przeliczalnie addytywnej na σ-algebrze zbiorów mierzalnych w sensie Lebesgue’a.
. Miara jest dodatnia, jeśli przyjmuje wartości dodatnie; jeśli dodatkowo m(Ω) = 1, wówczas jest to miara probabilistyczna. W matematyce i fizyce są badane też miary przyjmujące wartości w bardziej ogólnych przestrzeniach, np. miary spektralne. Podobnie jak przedstawiono wyżej, wprowadza się pojęcia funkcji f na Ω, mierzalnej względem σ-algebry M i jej całki względem miary m, ∫Ωfdm. Miara Lebesgue’a jest przykładem miary przeliczalnie addytywnej na σ-algebrze zbiorów mierzalnych w sensie Lebesgue’a.
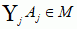 . Taka klasa nazywa się σ-algebrą (lub σ-ciałem). Przykładami są: σ-algebra podzbiorów ℝn mierzalnych w sensie Lebesgue’a i σ-algebra podzbiorów borelowskich (zbiór borelowski) przestrzeni metrycznej generowana przez podzbiory otwarte. Miarą przeliczalnie addytywną na M nazywa się funkcję m: M → ℝ o własności: jeśli A1, A2, ... ∈ M i Ai ∩ Aj = ∅, i ≠ j, to
. Taka klasa nazywa się σ-algebrą (lub σ-ciałem). Przykładami są: σ-algebra podzbiorów ℝn mierzalnych w sensie Lebesgue’a i σ-algebra podzbiorów borelowskich (zbiór borelowski) przestrzeni metrycznej generowana przez podzbiory otwarte. Miarą przeliczalnie addytywną na M nazywa się funkcję m: M → ℝ o własności: jeśli A1, A2, ... ∈ M i Ai ∩ Aj = ∅, i ≠ j, to 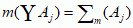 . Miara jest dodatnia, jeśli przyjmuje wartości dodatnie; jeśli dodatkowo m(Ω) = 1, wówczas jest to miara probabilistyczna. W matematyce i fizyce są badane też miary przyjmujące wartości w bardziej ogólnych przestrzeniach, np. miary spektralne. Podobnie jak przedstawiono wyżej, wprowadza się pojęcia funkcji f na Ω, mierzalnej względem σ-algebry M i jej całki względem miary m, ∫Ωfdm. Miara Lebesgue’a jest przykładem miary przeliczalnie addytywnej na σ-algebrze zbiorów mierzalnych w sensie Lebesgue’a.
. Miara jest dodatnia, jeśli przyjmuje wartości dodatnie; jeśli dodatkowo m(Ω) = 1, wówczas jest to miara probabilistyczna. W matematyce i fizyce są badane też miary przyjmujące wartości w bardziej ogólnych przestrzeniach, np. miary spektralne. Podobnie jak przedstawiono wyżej, wprowadza się pojęcia funkcji f na Ω, mierzalnej względem σ-algebry M i jej całki względem miary m, ∫Ωfdm. Miara Lebesgue’a jest przykładem miary przeliczalnie addytywnej na σ-algebrze zbiorów mierzalnych w sensie Lebesgue’a. Innym ważnym przykładem jest miara Lebesgue’a–Stjeltjesa dg, gdzie g jest funkcją na [a, b], mierzalną w sensie Lebesgue’a, o wahaniu skończonym (wahanie funkcji). Na odcinkach półotwartych (α, β] wynosi ona dg((α, β]) = g(β) − g(α). Analogicznie jak w przypadku całki Lebesgue’a są definiowane: miara zewn. i wewn. oraz zbiory mierzalne. Całka Lebesgue’a–Stjeltjesa 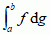 jest definiowana dla funkcji mierzalnych w sensie Lebesgue’a–Stjeltjesa. Gdy funkcja g jest stała poza skończoną lub przeliczalną liczbą punktów x1, x2, ... , to miara dg jest skupiona w tych punktach i ma postać ∑ai ·
jest definiowana dla funkcji mierzalnych w sensie Lebesgue’a–Stjeltjesa. Gdy funkcja g jest stała poza skończoną lub przeliczalną liczbą punktów x1, x2, ... , to miara dg jest skupiona w tych punktach i ma postać ∑ai · 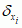 , gdzie liczby ai mierzą wysokości skoków g, a
, gdzie liczby ai mierzą wysokości skoków g, a 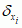 są (probabilistycznymi) miarami Diraca o nośnikach w xi. Punkty xi nazywają się atomami miary dg, a o samej mierze mówi się, że jest dyskretna. Gdy funkcja g jest absolutnie ciągła (tzn. ma określoną pochodną h = g′ poza zbiorem miary Lebesgue’a zero, pochodna ta jest całkowalna i dla dowolnego x
są (probabilistycznymi) miarami Diraca o nośnikach w xi. Punkty xi nazywają się atomami miary dg, a o samej mierze mówi się, że jest dyskretna. Gdy funkcja g jest absolutnie ciągła (tzn. ma określoną pochodną h = g′ poza zbiorem miary Lebesgue’a zero, pochodna ta jest całkowalna i dla dowolnego x 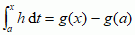 ), to całka Lebesgue’a–Stjeltjesa jest zwykłą całką Lebesgue’a ∫ f h. Może mieć miejsce pośrednia sytuacja, gdy miara dg nie jest dyskretna, ale jest skupiona na zbiorze o zerowej mierze Lebesgue’a. Mówi się wtedy, że dg jest ciągła osobliwa. Przykładem może być miara Lebesgue’a–Stjeltjesa skupiona na zbiorze Cantora C, miary Lebesgue’a zero:
), to całka Lebesgue’a–Stjeltjesa jest zwykłą całką Lebesgue’a ∫ f h. Może mieć miejsce pośrednia sytuacja, gdy miara dg nie jest dyskretna, ale jest skupiona na zbiorze o zerowej mierze Lebesgue’a. Mówi się wtedy, że dg jest ciągła osobliwa. Przykładem może być miara Lebesgue’a–Stjeltjesa skupiona na zbiorze Cantora C, miary Lebesgue’a zero: 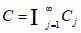 , gdzie C1 = [0, 1] i każdy zbiór Cj + 1 otrzymuje się z Cj przez wyrzucenie ze środka każdego odcinka [c, d], składającego się na Cj, otwartego pododcinka (c′, d′) o długości trzykrotnie krótszej. Funkcja Cantora g rośnie tylko na zbiorze C — jej wartość na (c′, d′) jest średnią między wartościami na lewo od c i na prawo od d.
, gdzie C1 = [0, 1] i każdy zbiór Cj + 1 otrzymuje się z Cj przez wyrzucenie ze środka każdego odcinka [c, d], składającego się na Cj, otwartego pododcinka (c′, d′) o długości trzykrotnie krótszej. Funkcja Cantora g rośnie tylko na zbiorze C — jej wartość na (c′, d′) jest średnią między wartościami na lewo od c i na prawo od d.
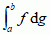 jest definiowana dla funkcji mierzalnych w sensie Lebesgue’a–Stjeltjesa. Gdy funkcja g jest stała poza skończoną lub przeliczalną liczbą punktów x1, x2, ... , to miara dg jest skupiona w tych punktach i ma postać ∑ai ·
jest definiowana dla funkcji mierzalnych w sensie Lebesgue’a–Stjeltjesa. Gdy funkcja g jest stała poza skończoną lub przeliczalną liczbą punktów x1, x2, ... , to miara dg jest skupiona w tych punktach i ma postać ∑ai · 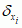 , gdzie liczby ai mierzą wysokości skoków g, a
, gdzie liczby ai mierzą wysokości skoków g, a 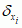 są (probabilistycznymi) miarami Diraca o nośnikach w xi. Punkty xi nazywają się atomami miary dg, a o samej mierze mówi się, że jest dyskretna. Gdy funkcja g jest absolutnie ciągła (tzn. ma określoną pochodną h = g′ poza zbiorem miary Lebesgue’a zero, pochodna ta jest całkowalna i dla dowolnego x
są (probabilistycznymi) miarami Diraca o nośnikach w xi. Punkty xi nazywają się atomami miary dg, a o samej mierze mówi się, że jest dyskretna. Gdy funkcja g jest absolutnie ciągła (tzn. ma określoną pochodną h = g′ poza zbiorem miary Lebesgue’a zero, pochodna ta jest całkowalna i dla dowolnego x 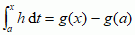 ), to całka Lebesgue’a–Stjeltjesa jest zwykłą całką Lebesgue’a ∫ f h. Może mieć miejsce pośrednia sytuacja, gdy miara dg nie jest dyskretna, ale jest skupiona na zbiorze o zerowej mierze Lebesgue’a. Mówi się wtedy, że dg jest ciągła osobliwa. Przykładem może być miara Lebesgue’a–Stjeltjesa skupiona na zbiorze Cantora C, miary Lebesgue’a zero:
), to całka Lebesgue’a–Stjeltjesa jest zwykłą całką Lebesgue’a ∫ f h. Może mieć miejsce pośrednia sytuacja, gdy miara dg nie jest dyskretna, ale jest skupiona na zbiorze o zerowej mierze Lebesgue’a. Mówi się wtedy, że dg jest ciągła osobliwa. Przykładem może być miara Lebesgue’a–Stjeltjesa skupiona na zbiorze Cantora C, miary Lebesgue’a zero: 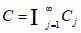 , gdzie C1 = [0, 1] i każdy zbiór Cj + 1 otrzymuje się z Cj przez wyrzucenie ze środka każdego odcinka [c, d], składającego się na Cj, otwartego pododcinka (c′, d′) o długości trzykrotnie krótszej. Funkcja Cantora g rośnie tylko na zbiorze C — jej wartość na (c′, d′) jest średnią między wartościami na lewo od c i na prawo od d.
, gdzie C1 = [0, 1] i każdy zbiór Cj + 1 otrzymuje się z Cj przez wyrzucenie ze środka każdego odcinka [c, d], składającego się na Cj, otwartego pododcinka (c′, d′) o długości trzykrotnie krótszej. Funkcja Cantora g rośnie tylko na zbiorze C — jej wartość na (c′, d′) jest średnią między wartościami na lewo od c i na prawo od d. Ważnymi przykładami miar są miary geom., zwłaszcza miara Jordana i miara Hausdorffa. Jeśli d jest liczbą dodatnią i diamΔ oznacza średnicę kostki sześciennej Δ ⊂ ℝn, to dla ograniczonego podzbioru A kostki G ⊂ ℝn definiuje się jego zewn. miarę Hausdorffa wymiaru d, me(A) jako granicę dolną liczb ∑, gdzie 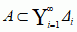 i diam(Δj) < ε → 0. Definicja miary wewn. i zbiorów mierzalnych jest taka sama jak powyżej. Odpowiednią miarę nazywa się miarą Hausdorffa zbioru A w wymiarze d i oznacza md. Jeśli 0 < md(A) < ∞, to liczba d = dH(A) jest wymiarem Hausdorffa zbioru A. Miara i wymiar Hausdorffa są skutecznymi narzędziami opisu zbiorów fraktalnych (fraktal) i zjawisk chaotycznych w układach dynamicznych i w przyrodzie, np. opisany zbiór Cantora jest przykładem zbioru o ułamkowym wymiarze Hausdorffa: dH(C) = ln2/ln3, mln2/ln3(C) = 1.
i diam(Δj) < ε → 0. Definicja miary wewn. i zbiorów mierzalnych jest taka sama jak powyżej. Odpowiednią miarę nazywa się miarą Hausdorffa zbioru A w wymiarze d i oznacza md. Jeśli 0 < md(A) < ∞, to liczba d = dH(A) jest wymiarem Hausdorffa zbioru A. Miara i wymiar Hausdorffa są skutecznymi narzędziami opisu zbiorów fraktalnych (fraktal) i zjawisk chaotycznych w układach dynamicznych i w przyrodzie, np. opisany zbiór Cantora jest przykładem zbioru o ułamkowym wymiarze Hausdorffa: dH(C) = ln2/ln3, mln2/ln3(C) = 1.
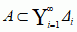 i diam(Δj) < ε → 0. Definicja miary wewn. i zbiorów mierzalnych jest taka sama jak powyżej. Odpowiednią miarę nazywa się miarą Hausdorffa zbioru A w wymiarze d i oznacza md. Jeśli 0 < md(A) < ∞, to liczba d = dH(A) jest wymiarem Hausdorffa zbioru A. Miara i wymiar Hausdorffa są skutecznymi narzędziami opisu zbiorów fraktalnych (fraktal) i zjawisk chaotycznych w układach dynamicznych i w przyrodzie, np. opisany zbiór Cantora jest przykładem zbioru o ułamkowym wymiarze Hausdorffa: dH(C) = ln2/ln3, mln2/ln3(C) = 1.
i diam(Δj) < ε → 0. Definicja miary wewn. i zbiorów mierzalnych jest taka sama jak powyżej. Odpowiednią miarę nazywa się miarą Hausdorffa zbioru A w wymiarze d i oznacza md. Jeśli 0 < md(A) < ∞, to liczba d = dH(A) jest wymiarem Hausdorffa zbioru A. Miara i wymiar Hausdorffa są skutecznymi narzędziami opisu zbiorów fraktalnych (fraktal) i zjawisk chaotycznych w układach dynamicznych i w przyrodzie, np. opisany zbiór Cantora jest przykładem zbioru o ułamkowym wymiarze Hausdorffa: dH(C) = ln2/ln3, mln2/ln3(C) = 1. T.m. przyczyniła się do rozwoju wielu dyscyplin nauk.: analizy funkcjonalnej (przestrzenie Lp i przestrzenie Sobolewa), analizy harmonicznej (szeregi Fouriera i miara Haara), teorii spektralnej operatorów (miary i typy spektralne), mechaniki kwantowej (całka Feynmana), teorii prawdopodobieństwa (aksjomatyzacja Kołmogorowa), układów dynamicznych (ergodyczność i mieszanie), równań różniczkowych cząstkowych (miara harmoniczna), mechaniki statyst. (miara Poissona dla gazu doskonałego, rozkłady Maxwella i Gibbsa) i kwantowej teorii pola. Rozwój teorii prawdopodobieństwa i fizyki mat. wymagał wprowadzenia miar na przestrzeniach nieskończenie wymiarowych. Są to przestrzenie typu Ω = ℝT, gdzie T jest zbiorem nieskończonym; np. gdy ma się do czynienia z ciągiem zmiennych losowych, to T jest zbiorem liczb naturalnych, natomiast dla procesu stochastycznego T = ℝ. Naturalną σ-algebrą dla tego typu modeli jest σ-algebra zbiorów cylindrycznych, generowana przez zbiory o postaci {(xt)t∈T: 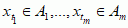 }, gdzie Aj ⊂ ℝ są zbiorami borelowskimi. Miara na tej σ-algebrze jest określona przez układ skończenie wymiarowych miar
}, gdzie Aj ⊂ ℝ są zbiorami borelowskimi. Miara na tej σ-algebrze jest określona przez układ skończenie wymiarowych miar 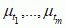 na ℝn spełniających pewne naturalne warunki zgodności (twierdzenie Kołmogorowa). Przykładem tak zdefiniowanej miary jest miara Wienera na przestrzeni Ω = ℝ[0, ∞) trajektorii ruchów Browna. Innych przykładów dostarczają graniczne miary Gibbsa z fizyki statyst., np. w modelu Isinga ferromagnetyku
na ℝn spełniających pewne naturalne warunki zgodności (twierdzenie Kołmogorowa). Przykładem tak zdefiniowanej miary jest miara Wienera na przestrzeni Ω = ℝ[0, ∞) trajektorii ruchów Browna. Innych przykładów dostarczają graniczne miary Gibbsa z fizyki statyst., np. w modelu Isinga ferromagnetyku 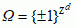 , natomiast miara Gibbsa jest granicą miar μΛ zadanych w skończonych obszarach Λ siatki całkowitoliczbowej ℤ d, μΛ((xt) const · exp(–β∑|t–s|=1|xt – xs|). W modelach mat. kwantowej teorii pola przestrzenią konfiguracji jest przestrzeń S′(ℝd) dystrybucji temperowanych (przestrzeń ciągłych funkcjonałów liniowych na przestrzeni S(ℝn) funkcji gładkich i szybko malejących w nieskończoności). Okazuje się, że na tej przestrzeni można określić σ-algebrę zbiorów cylindrycznych i miarę gaussowską, odpowiadającą swobodnemu polu skalarnych bozonów.
, natomiast miara Gibbsa jest granicą miar μΛ zadanych w skończonych obszarach Λ siatki całkowitoliczbowej ℤ d, μΛ((xt) const · exp(–β∑|t–s|=1|xt – xs|). W modelach mat. kwantowej teorii pola przestrzenią konfiguracji jest przestrzeń S′(ℝd) dystrybucji temperowanych (przestrzeń ciągłych funkcjonałów liniowych na przestrzeni S(ℝn) funkcji gładkich i szybko malejących w nieskończoności). Okazuje się, że na tej przestrzeni można określić σ-algebrę zbiorów cylindrycznych i miarę gaussowską, odpowiadającą swobodnemu polu skalarnych bozonów.
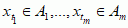 }, gdzie Aj ⊂ ℝ są zbiorami borelowskimi. Miara na tej σ-algebrze jest określona przez układ skończenie wymiarowych miar
}, gdzie Aj ⊂ ℝ są zbiorami borelowskimi. Miara na tej σ-algebrze jest określona przez układ skończenie wymiarowych miar 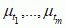 na ℝn spełniających pewne naturalne warunki zgodności (twierdzenie Kołmogorowa). Przykładem tak zdefiniowanej miary jest miara Wienera na przestrzeni Ω = ℝ[0, ∞) trajektorii ruchów Browna. Innych przykładów dostarczają graniczne miary Gibbsa z fizyki statyst., np. w modelu Isinga ferromagnetyku
na ℝn spełniających pewne naturalne warunki zgodności (twierdzenie Kołmogorowa). Przykładem tak zdefiniowanej miary jest miara Wienera na przestrzeni Ω = ℝ[0, ∞) trajektorii ruchów Browna. Innych przykładów dostarczają graniczne miary Gibbsa z fizyki statyst., np. w modelu Isinga ferromagnetyku 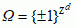 , natomiast miara Gibbsa jest granicą miar μΛ zadanych w skończonych obszarach Λ siatki całkowitoliczbowej ℤ d, μΛ((xt) const · exp(–β∑|t–s|=1|xt – xs|). W modelach mat. kwantowej teorii pola przestrzenią konfiguracji jest przestrzeń S′(ℝd) dystrybucji temperowanych (przestrzeń ciągłych funkcjonałów liniowych na przestrzeni S(ℝn) funkcji gładkich i szybko malejących w nieskończoności). Okazuje się, że na tej przestrzeni można określić σ-algebrę zbiorów cylindrycznych i miarę gaussowską, odpowiadającą swobodnemu polu skalarnych bozonów.
, natomiast miara Gibbsa jest granicą miar μΛ zadanych w skończonych obszarach Λ siatki całkowitoliczbowej ℤ d, μΛ((xt) const · exp(–β∑|t–s|=1|xt – xs|). W modelach mat. kwantowej teorii pola przestrzenią konfiguracji jest przestrzeń S′(ℝd) dystrybucji temperowanych (przestrzeń ciągłych funkcjonałów liniowych na przestrzeni S(ℝn) funkcji gładkich i szybko malejących w nieskończoności). Okazuje się, że na tej przestrzeni można określić σ-algebrę zbiorów cylindrycznych i miarę gaussowską, odpowiadającą swobodnemu polu skalarnych bozonów. Henryk Żołądek


