Drogi Użytkowniku AdBlocka,
wiemy, jak cenny jest Twój czas – zajmiemy Ci tylko chwilę.
Czy dasz nam szansę, abyśmy mogli dalej tworzyć źródło Twojej sprawdzonej, darmowej wiedzy, z której właśnie chcesz skorzystać? Bez wpływu z reklam będzie to po prostu niemożliwe.
Dlatego prosimy – dodaj naszą domenę, jako wyjątek lub skorzystaj z instrukcji i odblokuj wyświetlanie reklam na naszych serwisach.
Dziękujemy!
Redakcja serwisów PWN
Wydawnictwa Naukowego PWN
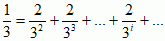 ;
;
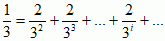 ;
;