Hausdorffa wymiar,
mat. nieujemna liczba rzeczywista r przypisana przestrzeni metrycznej X wg następującej procedury: 1) dla liczb rzeczywistych p ≥ 0 i d > 0 rozpatruje się pokrycia przestrzeni X kulami o środkach w punktach xi ∈ X i średnicach di ≤ d, i = 1, 2, ... (dopuszcza się również skończoną liczbę kul), 2) znajduje się kres dolny md liczb 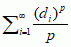 po wszystkich takich pokryciach i wylicza granicę
po wszystkich takich pokryciach i wylicza granicę 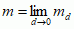 (m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).
(m jest tzw. p-wymiarową miarą Hausdorffa przestrzeni X), 3) jako r przyjmuje się taką liczbę, by m dla p > r było nieskończonością, dla p = r liczbą skończoną, a dla p < r (o ile r > 0) — równą 0 (tylko dla jednej wartości p miara Hausdorffa może być dodatnia i skończona).

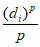 (funkcje Hausdorffa); może to prowadzić do innej wartości w.H. Wymiar przestrzeni nie będący liczbą całkowitą wprowadził F. Hausdorff (
(funkcje Hausdorffa); może to prowadzić do innej wartości w.H. Wymiar przestrzeni nie będący liczbą całkowitą wprowadził F. Hausdorff (
