przestrzeń metryczna,
mat. jedno z podstawowych pojęć matematyki: zbiór X wraz z funkcją ρ, zwaną metryką, przyporządkowującą każdej parze elementów x, y tego zbioru odległość między nimi ρ(x, y), przy czym dla dowolnych x, y, z ∈ X zachodzi: 1) ρ(x, y) = 0 wtedy i tylko wtedy, gdy x = y, 2) ρ(x, y) = ρ(y, x), 3) ρ(x, y) + ρ(y, z) ≥ ρ(x, z) (nierówność trójkąta).
- metryka
- przestrzeń topologiczna
- analiza funkcjonalna
- ciąg
- ciągłość funkcji
- zbiór domknięty
- granica
- Hausdorff Felix
- Hausdorffa wymiar
- Hilberta kostka
- izometria
- kontinuum
- kula
- nierówność trójkąta
- odcinek
- odległość
- zbiór ograniczony
- zbiór otwarty
- pochodna zbioru
- podobieństwo
- potok
- przestrzeń
- przybliżeń kolejnych metoda
- przestrzeń Riemanna
- średnica zbioru
- topologia geometryczna
- wnętrze zbioru
- zbieżność
- przestrzeń

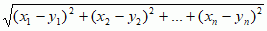 ; 3) zbiór liczb zespolonych
; 3) zbiór liczb zespolonych  z metryką ρ(z1, z2) = |z1 − z2|; 4) zbiór C([a, b]) wszystkich funkcji ciągłych określonych na przedziale domkniętym [a, b] o wartościach rzeczywistych, z metryką ρ(f, g) = max {|f(x) − g(x)|: x ∈ [a, b]}; 5) przestrzeń dyskretna — dowolny zbiór X, w którym odległość między różnymi punktami jest zawsze równa 1, a między punktem i nim samym = 0.
z metryką ρ(z1, z2) = |z1 − z2|; 4) zbiór C([a, b]) wszystkich funkcji ciągłych określonych na przedziale domkniętym [a, b] o wartościach rzeczywistych, z metryką ρ(f, g) = max {|f(x) − g(x)|: x ∈ [a, b]}; 5) przestrzeń dyskretna — dowolny zbiór X, w którym odległość między różnymi punktami jest zawsze równa 1, a między punktem i nim samym = 0.
