potok,
mat. termin teorii układów dynamicznych, spotykany także w zagadnieniach wywodzących się z teorii równań różniczkowych zwyczajnych, mechaniki, geometrii różniczkowej i in.
potok
Encyklopedia PWN
W najszerszym sensie p. to układ dynamiczny z przestrzenią fazową χ i rodziną (φt)t∈T odwzorowań tej przestrzeni w samą siebie, indeksowaną elementami grupy (ewentualnie półgrupy) T; odwzorowania te zachowują istniejącą w przestrzeni fazowej strukturę (np. miarę) oraz spełniają zależności φ0(x) = x, φt + s(x) = φt(φs(x)). W zastosowaniach χ to najczęściej przestrzeń metryczna lub gładka rozmaitość różniczkowa, a φ t to odwzorowanie ciągłe (lub różniczkowalne), natomiast T to wszystkie liczby rzeczywiste, ewentualnie półgrupa liczb rzeczywistych nieujemnych z elementem neutralnym 0; stąd indeksy t nazywa się czasem, a zależność x φt(x) — ruchem punktu x. P., w których zbiór T stanowią liczby całkowite (ewentualnie naturalne), noszą nazwę kaskad. Przykładem p. z przestrzenią fazową χ = ℝn jest ciągła grupa przekształceń liniowych, tzn. takich, że φt = At, przy czym dla każdego t ∈ ℝ odwzorowanie At: ℝn → ℝn jest liniowe oraz
φt(x) — ruchem punktu x. P., w których zbiór T stanowią liczby całkowite (ewentualnie naturalne), noszą nazwę kaskad. Przykładem p. z przestrzenią fazową χ = ℝn jest ciągła grupa przekształceń liniowych, tzn. takich, że φt = At, przy czym dla każdego t ∈ ℝ odwzorowanie At: ℝn → ℝn jest liniowe oraz 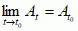 ; istnieje wówczas jedno przekształcenie liniowe L: ℝn → ℝn, takie że wszystkie przekształcenia At w tym potoku są postaci At = etL.
; istnieje wówczas jedno przekształcenie liniowe L: ℝn → ℝn, takie że wszystkie przekształcenia At w tym potoku są postaci At = etL.
 φt(x) — ruchem punktu x. P., w których zbiór T stanowią liczby całkowite (ewentualnie naturalne), noszą nazwę kaskad. Przykładem p. z przestrzenią fazową χ = ℝn jest ciągła grupa przekształceń liniowych, tzn. takich, że φt = At, przy czym dla każdego t ∈ ℝ odwzorowanie At: ℝn → ℝn jest liniowe oraz
φt(x) — ruchem punktu x. P., w których zbiór T stanowią liczby całkowite (ewentualnie naturalne), noszą nazwę kaskad. Przykładem p. z przestrzenią fazową χ = ℝn jest ciągła grupa przekształceń liniowych, tzn. takich, że φt = At, przy czym dla każdego t ∈ ℝ odwzorowanie At: ℝn → ℝn jest liniowe oraz 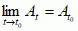 ; istnieje wówczas jedno przekształcenie liniowe L: ℝn → ℝn, takie że wszystkie przekształcenia At w tym potoku są postaci At = etL.
; istnieje wówczas jedno przekształcenie liniowe L: ℝn → ℝn, takie że wszystkie przekształcenia At w tym potoku są postaci At = etL. P. na rozmaitościach różniczkowych są powiązane z polami wektorowymi. Gdy χ jest rozmaitością różniczkową (np. gładką rozmaitością bez brzegu, jak sfera czy torus), a (φt)t∈ℝ — p. dyfeomorfizmów tej rozmaitości, to taki p. określa na rozmaitości pole wektorowe V zadane wzorem V(x) = 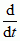 φt(x); na odwrót, na zwartej rozmaitości pole wektorowe (lub odpowiadające mu równanie różniczkowe zwyczajne
φt(x); na odwrót, na zwartej rozmaitości pole wektorowe (lub odpowiadające mu równanie różniczkowe zwyczajne 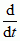 x(t) = v(x)) zadaje p. W mechanice dla układu, którego ewolucja jest opisana równaniem różniczkowym Lagrange’a (Lagrange’a równania ruchu), generowanie p. przez równanie różniczkowe prowadzi (przy odpowiednim wyborze zmiennej czasowej) do pojęcia p. geodezyjnego.
x(t) = v(x)) zadaje p. W mechanice dla układu, którego ewolucja jest opisana równaniem różniczkowym Lagrange’a (Lagrange’a równania ruchu), generowanie p. przez równanie różniczkowe prowadzi (przy odpowiednim wyborze zmiennej czasowej) do pojęcia p. geodezyjnego.
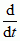 φt(x); na odwrót, na zwartej rozmaitości pole wektorowe (lub odpowiadające mu równanie różniczkowe zwyczajne
φt(x); na odwrót, na zwartej rozmaitości pole wektorowe (lub odpowiadające mu równanie różniczkowe zwyczajne 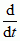 x(t) = v(x)) zadaje p. W mechanice dla układu, którego ewolucja jest opisana równaniem różniczkowym Lagrange’a (Lagrange’a równania ruchu), generowanie p. przez równanie różniczkowe prowadzi (przy odpowiednim wyborze zmiennej czasowej) do pojęcia p. geodezyjnego.
x(t) = v(x)) zadaje p. W mechanice dla układu, którego ewolucja jest opisana równaniem różniczkowym Lagrange’a (Lagrange’a równania ruchu), generowanie p. przez równanie różniczkowe prowadzi (przy odpowiednim wyborze zmiennej czasowej) do pojęcia p. geodezyjnego. Najważniejsze zagadnienia związane z analizowaniem własności p. to badanie istnienia orbit zamkniętych (okresowych) i zachowania się p. w otoczeniach takich orbit, a także analiza stabilności, tzn. badanie, czy zachowanie p. bliskich danemu podlega zmianom jakościowym przy niewielkich zaburzeniach. Z operacji różniczkowania p. w kierunku pola wektorowego wywodzi się ważne w geometrii różniczkowej pojęcie nawiasu Liego. Od zarania teorii układów dynamicznych p. były najczęściej i najintensywniej badanymi układami, stąd też samo pojęcie układu dynamicznego bywa również utożsamiane z pojęciem p.
Waldemar Pałuba


