Lagrange’a równania ruchu,
fiz. równania różniczkowe opisujące ruch układu mech. swobodnego lub z więzami dwustronnymi (więzy);
Lagrange’a równania ruchu
Encyklopedia PWN
R.r.L. pierwszego rodzaju są zapisane za pomocą współrz. prostokątnego układu współrz. i zawierają tzw. mnożniki Lagrange’a λk; dla układu n punktów materialnych o p więzach określonych funkcjami fkj = fkj(x1, x2, ... , x3n, t) mają postać:
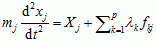 (j = 1, 2, ... , 3n),
(j = 1, 2, ... , 3n),
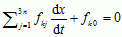 (k = 1, 2, ... , p),
(k = 1, 2, ... , p),
 (i = 1, 2, ... , f),
(i = 1, 2, ... , f),
 (i = 1, 2, ... , f),
(i = 1, 2, ... , f),
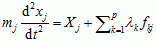 (j = 1, 2, ... , 3n),
(j = 1, 2, ... , 3n), 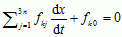 (k = 1, 2, ... , p),
(k = 1, 2, ... , p), gdzie: mj — masy, xj — współrz. punktów materialnych, Xj — składowe sił czynnych działających na te punkty, t — czas. Rozwiązanie r.r.L. pozwala określić ruch układu oraz siły reakcji więzów odpowiadające w równaniach ruchu członom z mnożnikami Lagrange’a. R.r.L. drugiego rodzaju są zapisane we współrz. uogólnionych i dla układu z więzami holonomicznymi doskonałymi mają postać:
 (i = 1, 2, ... , f),
(i = 1, 2, ... , f), przy czym: qi, &qdot.x;i = dqi /dt — współrz. i prędkości uogólnione, T = T(qi, &qdot.x;i, t) — energia kinet., Qi = Qi (qi, &qdot.x;i, t) — siły uogólnione, f — liczba stopni swobody układu; gdy Qi mają uogólnioną energię potencjalną U, równania ruchu Lagrange’a drugiego rodzaju przyjmują postać:
 (i = 1, 2, ... , f),
(i = 1, 2, ... , f), gdzie L — funkcja Lagrange’a. Równania ruchu Lagrange’a są stosowane m.in. w teorii drgań i dynamice mechanizmów oraz maszyn; wprowadzone do mechaniki 1788 przez J.L. de Lagrange’a.


