mechanika

mechanika

[gr. mēchanikḗ ‘sztuka konstruowania maszyn’],

dział fizyki zajmujący się badaniem ruchu ciał materialnych oraz oddziaływań między nimi, prowadzących do zmiany ruchu ciał lub ich odkształceń.

Analizą ruchu i oddziaływań ciał w świecie makroskopowym zajmuje się mechanika klasyczna, a w świecie mikroskopowym (w skali cząsteczkowej, atomowej, jądrowej itd.) mechanika kwantowa. Analizą ruchu i oddziaływań ciał poruszających się z prędkościami małymi w stosunku do prędkości światła w próżni zajmuje się mechanika nierelatywistyczna, a analizą przy dowolnych prędkościach (także bliskich prędkości światła w próżni) mechanika relatywistyczna. Mechanika stanowi podstawę licznych zastosowań technicznych.

Ze względu na sposób podejścia do przedmiotu badań rozróżnia się mechanikę teoretyczną, doświadczalną i stosowaną, ze względu zaś na problematykę rozwiązywanych zagadnień kinematykę i dynamikę (obejmującą kinetykę i statykę). W zależności od właściwości badanych obiektów rozróżnia się: mechanikę punktu materialnego i układu punktów materialnych, mechanikę bryły sztywnej i mechanikę ośrodków ciągłych, która z kolei dzieli się na mechanikę płynów (hydromechanika, aerodynamika) oraz mechanikę ciał stałych, np. odkształcalnych sprężyście lub plastycznie. Mechanika klasyczna nierelatywistyczna jest oparta na zasadach dynamiki Newtona. Prawa mechaniki relatywistycznej są niezmiennicze względem przekształceń Lorentza i słuszne dla dowolnych prędkości; w przypadku prędkości małych w porównaniu z prędkością światła w próżni prawa te przechodzą w prawa mechaniki nierelatywistycznej. 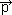II zasada dynamiki ma w mechanice relatywistycznej postać d  / dt = 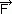, przy czym pęd jest dany wzorem  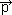= m_r(v)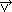, gdzie m_r(v) — masa relatywistyczna zależna od prędkości v (jest to również jedna z możliwych postaci II zasady w mechanice nierelatywistycznej). Mechanika operuje związkami przyczynowo-skutkowymi: stan początkowy układu określa całkowicie każdy stan późniejszy układu. Podstawowymi prawami mechaniki są prawa zachowania pewnych wielkości mechanicznych: energii, pędu, momentu pędu. Do opisu ruchu układu mechanicznego stosuje się równanie Newtona, równania Lagrange’a (Lagrange’a równania ruchu), równania Hamiltona (Hamiltona równania ruchu), równanie Hamiltona–Jacobiego i in. Rozwój mechaniki datuje się od starożytności (Arystoteles, Archimedes); głównymi twórcami nowożytnej matematyki byli: Galileusz, I. Newton, J. d’Alembert, J.L. Lagrange, W.R. Hamilton, D. Bernoulli, B.P. Clapeyron, L. Euler, A. Einstein.