mechanika kwantowa,
fundamentalna teoria fizyczna opisująca oddziaływanie mikroobiektów materii między sobą oraz z zewnętrznymi polami, głównie z polem elektromagnetycznym.
mechanika kwantowa
Encyklopedia PWN
Mechanika kwantowa jest przede wszystkim teorią atomów i cząstek, w której nie odgrywają roli procesy kreacji i anihilacji par cząstek, opisane przez ogólniejszą teorię, zwaną kwantową teorią pola. Mechanika kwantowa powstała z tzw. starszej teorii kwantów; podstawy mechaniki kwantowej stworzyli: E. Schrödinger (1926), posługujący się hipotezą de Broglie’a o falowej naturze mikrocząstek (fale de Broglie’a) oraz prawie jednocześnie — W. Heisenberg (1925) i P.A.M. Dirac, którzy podali równoważne, ale posługujące się innymi formalizmami matematycznymi, postacie mechaniki kwantowej; do rozwoju mechaniki kwantowej przyczynili się M. Born i W. Pauli. Mechanika kwantowa nie jest zaprzeczeniem mechaniki klasycznej; jest ona teorią ogólniejszą i obejmuje mechanikę klasyczną jako graniczny przypadek, gdy układy są złożone z ciał o dużych masach (ciał makroskopowych). W mechanice klasycznej wielkości dynamiczne są reprezentowane przez operatory, np. składowe pędu cząstki przez operatory:
 ,
,  ,
,  ,
,
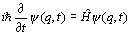 ,
,
 ,
,  ,
,  ,
, a całkowita energia przez operator zwany hamiltonianem Ĥ. Wszystkie wartości liczbowe, które można otrzymać dokonując pomiaru wielkości fizycznej, są dane poprzez wartości własne odpowiedniego operatora Ô, a więc takie liczby rzeczywiste on, że dla każdej z nich istnieje ciągła, jednoznaczna i ograniczona funkcja fn(q) współrzędnej q, spełniająca równanie: Ôfn(q) = onfn(q).
Funkcje fn(q) nazywają się funkcjami własnymi operatora i można ich używać do określania stanu kwantowego układu. W szczególności funkcje własne hamiltonianu Ĥ nazywają się funkcjami falowymi układu (funkcja falowa ψ (q, t) opisuje stan cząstki w danej chwili i jest na ogół funkcją zespoloną czasu i współrzędnych przestrzennych cząstki). Funkcje falowe są rozwiązaniem równania Schrödingera:
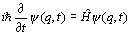 ,
, które w mechanice kwantowej gra rolę równania ruchu. Relatywistycznym uogólnieniem równania Schrödingera jest równanie Kleina–Gordona; relatywistycznym równaniem ruchu dla cząstek o spinie 1/2 jest równanie Diraca. Mechanika kwantowa stanowi podstawową teorię współczesnej fizyki; jej rozwój miał również doniosłe znaczenie dla filozofii.


