przestrzeń Hilberta,
mat. jedno z podstawowych pojęć analizy funkcjonalnej; szczególny przypadek przestrzeni Banacha; p.H. jest przestrzenią unitarną zupełną (przestrzeń unitarna, przestrzeń zupełna ) z normą 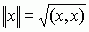 , gdzie (x, x) jest iloczynem skalarnym.
, gdzie (x, x) jest iloczynem skalarnym.

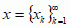 , gdzie x = (x1, x2, ... , xn), y = (y1, y2, ... , yn) — punkty tej przestrzeni, a kreska oznacza sprzężenie zespolone; 2) przestrzeń l2 wszystkich ciągów zespolonych
, gdzie x = (x1, x2, ... , xn), y = (y1, y2, ... , yn) — punkty tej przestrzeni, a kreska oznacza sprzężenie zespolone; 2) przestrzeń l2 wszystkich ciągów zespolonych 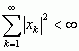 , spełniających warunek
, spełniających warunek 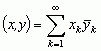 ; 3) przestrzeń L2([0, 1]) wszystkich funkcji całkowalnych z kwadratem na odcinku [0, 1], z iloczynem skalarnym
; 3) przestrzeń L2([0, 1]) wszystkich funkcji całkowalnych z kwadratem na odcinku [0, 1], z iloczynem skalarnym 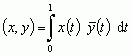 .
.
