przestrzeń Banacha

przestrzeń Banacha,

mat. jedno z najważniejszych pojęć analizy funkcjonalnej: przestrzeń liniowa, unormowana (odległość ρ(x, y) dwóch jej elementów x, y określa się jako normę ich różnicy: ρ(x, y) = ∥x − y∥) i zupełna (tzn. każdy ciąg (x_n) elementów przestrzeni Banacha X, który spełnia warunek Cauchy’ego 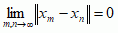ma granicę: istnieje element x ∈ X, taki że ).

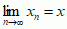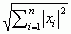Po raz pierwszy systematycznie badana przez S. Banacha (od 1922). Przykładami przestrzeni Banacha są: przestrzeń euklidesowa n-wymiarowa E_n z normą ||(x₁, x₂, ... , x_n)|| = ; przestrzeń C[0,1] wszystkich funkcji ciągłych na odcinku [0,1] z normą ||x(t)|| = max|x(t)| (maksimum wartości bezwzględnej funkcji x(t) na odcinku [0,1]); przestrzeń l_p wszystkich ciągów {x_n} z normą ||x_n|| =  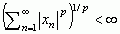(p ≥ 1). Przestrzeń Banacha, która jest jednocześnie pierścieniem, a mnożenie z tego pierścienia jest ciągłe, nazywa się algebrą Banacha; pojęcie to wprowadził (1941) i podał jego podstawowe własności I.M. Gelfand. Algebry Banacha, a dokładniej — pewne ich szczególne klasy, stanowią ważne narzędzie mechaniki kwantowej.