przestrzenie Sobolewa,
mat. przestrzenie Banacha złożone z tych funkcji całkowalnych z p-tą potęgą, których wszystkie dystrybucyjne pochodne cząstkowe, do ustalonego rzędu włącznie, również są całkowalne z p-tą potęgą;
przestrzenie Sobolewa
Encyklopedia PWN
ściślej, jeśli Ω jest obszarem w ℝn, k ≥ 1 jest liczbą naturalną, a p ∈ [1, ∞], to p.S. Wk, p(Ω) składa się z tych funkcji u ∈ Lp(Ω), których pochodne dystrybucyjne Dαu należą do Lp(Ω) dla wszystkich multiindeksów α = (α1, ... , αn) długości |α| = α1 + ... + αn ≤ k; mówi się przy tym, że Dαu = w, jeśli istnieje taka lokalnie całkowalna funkcja w, że dla wszystkich gładkich funkcji próbnych φ ∈ C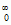 (Ω) zachodzi równość ʧΩ uDαφdx = (−1)|α| ʧΩ wφdx. Norma funkcji u w przestrzeni Wk, p(Ω) jest sumą norm u i jej wszystkich pochodnych cząstkowych do rzędu k włącznie w przestrzeni Lp(Ω). Jeśli Ω jest ograniczony i ma gładki brzeg, to zbiór C ∞(
(Ω) zachodzi równość ʧΩ uDαφdx = (−1)|α| ʧΩ wφdx. Norma funkcji u w przestrzeni Wk, p(Ω) jest sumą norm u i jej wszystkich pochodnych cząstkowych do rzędu k włącznie w przestrzeni Lp(Ω). Jeśli Ω jest ograniczony i ma gładki brzeg, to zbiór C ∞(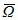 ) funkcji gładkich na domknięciu obszaru Ω jest gęstym podzbiorem przestrzeni Wk, p(Ω). Gęstym podzbiorem Wk, p(ℝn) jest C
) funkcji gładkich na domknięciu obszaru Ω jest gęstym podzbiorem przestrzeni Wk, p(Ω). Gęstym podzbiorem Wk, p(ℝn) jest C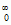 (ℝn).
(ℝn).
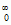 (Ω) zachodzi równość ʧΩ uDαφdx = (−1)|α| ʧΩ wφdx. Norma funkcji u w przestrzeni Wk, p(Ω) jest sumą norm u i jej wszystkich pochodnych cząstkowych do rzędu k włącznie w przestrzeni Lp(Ω). Jeśli Ω jest ograniczony i ma gładki brzeg, to zbiór C ∞(
(Ω) zachodzi równość ʧΩ uDαφdx = (−1)|α| ʧΩ wφdx. Norma funkcji u w przestrzeni Wk, p(Ω) jest sumą norm u i jej wszystkich pochodnych cząstkowych do rzędu k włącznie w przestrzeni Lp(Ω). Jeśli Ω jest ograniczony i ma gładki brzeg, to zbiór C ∞(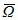 ) funkcji gładkich na domknięciu obszaru Ω jest gęstym podzbiorem przestrzeni Wk, p(Ω). Gęstym podzbiorem Wk, p(ℝn) jest C
) funkcji gładkich na domknięciu obszaru Ω jest gęstym podzbiorem przestrzeni Wk, p(Ω). Gęstym podzbiorem Wk, p(ℝn) jest C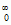 (ℝn).
(ℝn). Dla p = 2 przestrzenie Wk, 2(ℝn) (oznaczane także Hk(ℝn)) definiuje się równoważnie za pomocą transformaty Fouriera (Fouriera przekształcenie); mianowicie: u ∈ Wk, 2(ℝn) wtedy i tylko wtedy, gdy transformata Fouriera û spełnia warunek 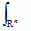 |û(ξ)|2 (1+|ξ|2)k/2dξ < + ∞; wartość powyższej całki jest równoważną normą w Wk, 2. Ta definicja ma sens także dla niecałkowitych wartości k.
|û(ξ)|2 (1+|ξ|2)k/2dξ < + ∞; wartość powyższej całki jest równoważną normą w Wk, 2. Ta definicja ma sens także dla niecałkowitych wartości k.
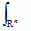 |û(ξ)|2 (1+|ξ|2)k/2dξ < + ∞; wartość powyższej całki jest równoważną normą w Wk, 2. Ta definicja ma sens także dla niecałkowitych wartości k.
|û(ξ)|2 (1+|ξ|2)k/2dξ < + ∞; wartość powyższej całki jest równoważną normą w Wk, 2. Ta definicja ma sens także dla niecałkowitych wartości k. P.S. mają liczne zastosowania we współcz. teorii równań różniczkowych i rachunku wariacyjnym, m.in. dlatego, że za ich pomocą można oddzielić pytania o istnienie (odpowiednio zdefiniowanych) rozwiązań równań różniczkowych i zagadnień wariacyjnych od pytań o klasycznie rozumianą gładkość tych rozwiązań.


