wariacyjny rachunek,
mat. dział analizy mat., który zajmuje się wyznaczaniem ekstremów i punktów kryt. funkcjonałów, tzn. wielkości zmiennych, definiowanych w taki sposób, że każdej funkcji u (lub krzywej, powierzchni itp.), należącej do ustalonej klasy, odpowiada liczba I[u], będąca wartością pewnej całki, np. (1) I[u] = ∫Ω F(x, u(x), Du(x))dx (rozpatruje się także zagadnienia wariacyjne, w których funkcja F zależy od pochodnych wyższych rzędów funkcji u).
wariacyjny rachunek
Encyklopedia PWN
w najprostszym przypadku funkcjonał J wyraża się następującą całką oznaczoną:
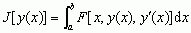 ,
,
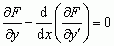 ; istnieją również określone warunki dostateczne, by znaleziona z tego równania funkcja y(x) nadawała rozważanemu funkcjonałowi J minimum (lub maksimum). Jednym z pierwszych zagadnień tego typu było zagadnienie brachistochrony; odpowiedni funkcjonał ma postać:
; istnieją również określone warunki dostateczne, by znaleziona z tego równania funkcja y(x) nadawała rozważanemu funkcjonałowi J minimum (lub maksimum). Jednym z pierwszych zagadnień tego typu było zagadnienie brachistochrony; odpowiedni funkcjonał ma postać:
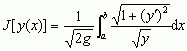 .
.
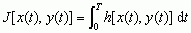 ,
,
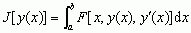 ,
,gdzie F jest znaną funkcją argumentów x, y i y′, zaś y(x) — szukaną funkcją zmiennej x, a granice całkowania a i b są stałe; dla różnych funkcji y(x) funkcjonał J przyjmuje różne wartości; chodzi o znalezienie takiej funkcji y(x), dla której funkcjonał J przyjmuje wartość najmniejszą lub największą (czyli ekstremalną), przy czym to ekstremum rozumie się w sposób następujący: ustala się pewną klasę funkcji dopuszczalnych do porównywania i twierdzi się, że funkcjonał J osiąga dla funkcji 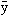 (x) minimum, jeżeli dla każdej funkcji y(x) należącej do wspomnianej klasy zachodzi nierówność J[y(x)] ≤ J[
(x) minimum, jeżeli dla każdej funkcji y(x) należącej do wspomnianej klasy zachodzi nierówność J[y(x)] ≤ J[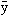 (x)]; podobnie definiuje się maksimum funkcjonału; dowodzi się, że jeżeli dla pewnej funkcji y(x) funkcjonał J przybiera wartość ekstremalną, to funkcja y(x) spełnia tzw. równanie różniczkowe Lagrange’a–Eulera
(x)]; podobnie definiuje się maksimum funkcjonału; dowodzi się, że jeżeli dla pewnej funkcji y(x) funkcjonał J przybiera wartość ekstremalną, to funkcja y(x) spełnia tzw. równanie różniczkowe Lagrange’a–Eulera
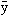 (x) minimum, jeżeli dla każdej funkcji y(x) należącej do wspomnianej klasy zachodzi nierówność J[y(x)] ≤ J[
(x) minimum, jeżeli dla każdej funkcji y(x) należącej do wspomnianej klasy zachodzi nierówność J[y(x)] ≤ J[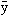 (x)]; podobnie definiuje się maksimum funkcjonału; dowodzi się, że jeżeli dla pewnej funkcji y(x) funkcjonał J przybiera wartość ekstremalną, to funkcja y(x) spełnia tzw. równanie różniczkowe Lagrange’a–Eulera
(x)]; podobnie definiuje się maksimum funkcjonału; dowodzi się, że jeżeli dla pewnej funkcji y(x) funkcjonał J przybiera wartość ekstremalną, to funkcja y(x) spełnia tzw. równanie różniczkowe Lagrange’a–Eulera
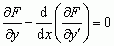 ; istnieją również określone warunki dostateczne, by znaleziona z tego równania funkcja y(x) nadawała rozważanemu funkcjonałowi J minimum (lub maksimum). Jednym z pierwszych zagadnień tego typu było zagadnienie brachistochrony; odpowiedni funkcjonał ma postać:
; istnieją również określone warunki dostateczne, by znaleziona z tego równania funkcja y(x) nadawała rozważanemu funkcjonałowi J minimum (lub maksimum). Jednym z pierwszych zagadnień tego typu było zagadnienie brachistochrony; odpowiedni funkcjonał ma postać: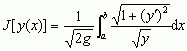 .
.Rachunek wariacyjny jest podstawą tzw. programowania nieliniowego (programowanie, optymalizacja). Podobnie jedno z podstawowych zagadnień teorii optymalnego sterowania sprowadza się do minimalizacji funkcjonału
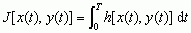 ,
,przy warunku dodatkowym w postaci równania różniczkowego dx/dt = h(x, y), x(0) = c, przy czym funkcja x(t) opisuje stan układu, a y(t) — sterowanie; rzadko tego typu zagadnienia dają się rozwiązać w sposób ścisły, często trzeba się uciekać do metod przybliżonych.
Początki rachunku wariacyjnego sięgają 1696, kiedy Johann i Jakob Bernoulli rozwiązali zagadnienie brachistochrony; zagadnieniami rachunku wariacyjnego zajmowali się matematycy, m.in.: L. Euler, J. Lagrange, M. Ostrogradski, C.F. Gauss, A.M. Legendre, C.G.J. Jacobi, K. Weierstrass; zainteresowanie rachunkiem wariacyjnym w fizyce i technice jest związane w znacznym stopniu z wariacyjnymi zagadnieniami mechaniki, a w ostatnim okresie zwłaszcza z problemami optymalizacji (optymalne sterowanie, optymalne kształtowanie wytrzymałościowe itp.).


