są to warunki wyróżniające rzeczywisty ruch układu fiz., zachodzący pod działaniem danych sił, spośród wielu innych kinematycznie możliwych (porównawczych) ruchów zgodnych z więzami. Wariacyjne zasady mechaniki można podzielić na całkowe, które analizują ruchy odbywające się w przedziale czasu (t0, t1) między tymi samymi dwoma (określonymi przez współrzędne uogólnione qi0 i qi1) położeniami układu, i różniczkowe, które analizują ruchy odbywające się w danej chwili.
Całkowe wariacyjne zasady mechaniki orzekają, że ruchem rzeczywistym układu fiz. jest ten, dla którego funkcjonał całkowy, zw.
działaniem, osiąga wartość stacjonarną, zwykle — minimalną (stąd stosowana również nazwa wariacyjnych zasad mechaniki — zasady najmniejszego działania); matematycznie wariacyjne zasady mechaniki wyraża równanie:
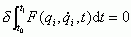
, przy czym funkcja podcałkowa
F nie musi w sposób jawny zależeć od czasu
t, a czas może być traktowany jako zmienna nie poddana wariacji (wariacyjne zasady mechaniki bez wariacji czasu, np. zasada Hamiltona) albo może być uważany za funkcję jakiejś innej, niezależnej zmiennej
τ i poddany wariacji (wariacyjne zasady mechaniki z wariacją czasu, np. zasada Maupertuisa).
Zasada Hamiltona porównuje ruchy układu zachodzące w tym samym przedziale czasu (
t0,
t1); jako funkcję
F przyjmuje
funkcję Lagrange’a.
Zasada Maupertuisa nie nakłada warunków na czas ruchów porównawczych; za funkcję
F przyjmuje energię kinet.
T układu, przy czym ruch rzeczywisty wybiera z klasy ruchów porównawczych spełniających dodatkowy warunek
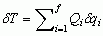
, reprezentujący bilans energii w danym układzie fiz. (
Qi — składowe sił uogólnionych,
f — liczba stopni swobody układu).
Zasada Jacobiego stanowi inną formę zasady Maupertuisa, zastosowaną do układów o więzach skleronomicznych, na które działają siły zachowawcze; za funkcję podcałkową
F przyjmuje funkcję Jacobiego, a całkowanie odbywa się po
τ. Całkowe wariacyjne zasady mechaniki doprowadzają do
równań Lagrange’a–Eulera odpowiednich zagadnień.
Wariacyjne zasady mechaniki pozwalają na stosunkowo proste sformułowanie równań ruchu skomplikowanych układów fiz., ponadto — przy odpowiednim uogólnieniu pojęć — mogą być stosowane w innych działach fizyki teoret. (np. w teorii pola, elektrodynamice, termodynamice)
W.z. stosuje się również w mechanice kwantowej, gdzie energia układu związanego osiąga minimum, gdy układ jest w stanie podstawowym.

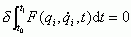 , przy czym funkcja podcałkowa F nie musi w sposób jawny zależeć od czasu t, a czas może być traktowany jako zmienna nie poddana wariacji (wariacyjne zasady mechaniki bez wariacji czasu, np. zasada Hamiltona) albo może być uważany za funkcję jakiejś innej, niezależnej zmiennej τ i poddany wariacji (wariacyjne zasady mechaniki z wariacją czasu, np. zasada Maupertuisa).
, przy czym funkcja podcałkowa F nie musi w sposób jawny zależeć od czasu t, a czas może być traktowany jako zmienna nie poddana wariacji (wariacyjne zasady mechaniki bez wariacji czasu, np. zasada Hamiltona) albo może być uważany za funkcję jakiejś innej, niezależnej zmiennej τ i poddany wariacji (wariacyjne zasady mechaniki z wariacją czasu, np. zasada Maupertuisa). 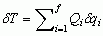 , reprezentujący bilans energii w danym układzie fiz. (Qi — składowe sił uogólnionych, f — liczba stopni swobody układu).
, reprezentujący bilans energii w danym układzie fiz. (Qi — składowe sił uogólnionych, f — liczba stopni swobody układu). 
