Urodził się 15 IV 1707 w Bazylei. Pierwszym nauczycielem Eulera był jego ojciec, Paul, pastor kalwiński w Riehen, uczeń Jakoba Bernoulliego. Mając 14 lat Euler wstąpił na uniwersytet w Bazylei, gdzie studiował teologię, języki klasyczne i historię. W 1723 uzyskał magisterium z filozofii, następnie zajął się matematyką i fizyką. Był uczniem J. Bernoulliego. Po nieudanej próbie uzyskania profesury z fizyki w Bazylei, 1727 otrzymał, dzięki protekcji D. Bernoulliego, stanowisko adiunkta w Akademii Nauk w Petersburgu, następnie został tam profesorem fizyki (1731–33), a 1733 — profesorem matematyki. Brał udział w przeprowadzanej w Rosji reformie miar i wag, był autorem podręcznika matematyki elementarnej dla szkół, pracował nad mapą Rosji. W 1735 stracił wzrok w jednym oku.
Ze względu na niepewną sytuację polityczną w Rosji po śmierci carycy Anny Iwanowny (1740), Euler przyjął zaproszenie Fryderyka II Hohenzollerna i na 25 lat przeniósł się do Berlina, gdzie pracował w Pruskiej Akademii Nauk (w latach 1744–66 kierował jej klasą matematyczną). W tym okresie powstał m.in. popularny zbiór wykładów z nauk przyrodniczych Lettres a une princesse d’Allemagne sur divers sujets de physique et philosophie [‘listy do niemieckiej księżniczki o różnych problemach filozofii i fizyki’ t. 1–3 1768–72]. W 1766 skorzystał z zaproszenia Katarzyny Wielkiej i powrócił do Petersburga, gdzie pozostał do śmierci. W 1771, po nieudanej operacji, utracił wzrok w drugim oku, mimo to był do końca aktywny naukowo. W pracy korzystał m.in. z pomocy synów, którym dyktował swoje prace. Zmarł 18 IX 1783 w Petersburgu (podczas zabawy z wnukiem dostał wylewu), po dniu spędzonym na pracy dotyczącej niedługo wcześniej odkrytego Urana. Petersburska Akademia Nauk jeszcze przez niemal 50 lat po śmierci Eulera drukowała jego niepublikowane prace w swoich rocznikach.
Badania Eulera miały ogromny wpływ na wszystkie działy matematyki oraz na jej zastosowania w fizyce. Jako pierwszy zastosował równania różniczkowe do mechaniki (
Mechanica sive motus scientia analytice exposita 1736) — opisał nimi ruch bąka. Stosował je także do optyki i hydrodynamiki. Napisał pierwszy podręcznik rachunku wariacyjnego (
Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes 1744). W dużym cyklu dzieł (
Introductio in analysin infinitorum 1748,
Institutiones calculi differentialis 1755,
Institutiones calculi integralis 1768–94) Euler przedstawił swoje teorie funkcji, ciągów i szeregów, rozpatrując zarówno przypadek rzeczywisty, jak i zespolony, oraz przedstawił ich zastosowania do równań różniczkowych i geometrii, co stało się początkiem geometrii różniczkowej. Całość znanej wówczas algebry przedstawił Euler w
Vollständige Anleitungzur Algebra (1770), a w kilkudziesięciu pracach z teorii liczb wprowadził m.in. funkcję dzeta
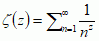
(co uznaje się za początek analitycznej teorii liczb), udowodnił istnienie pierwiastków pierwotnych liczb pierwszych, sformułował prawo wzajemności reszt kwadratowych i rozstrzygnął wiele problemów postawionych przez P. Fermata. Odkrył wieloznaczność logarytmu zespolonego, wprowadził do dziś używane symbole dla liczb: i, e, oraz udowodnił związek 1+e
iπ = 0, zachodzący między nimi. Odkrył też wiele innych wzorów matematycznych, z których najsławniejszy to: 1 + 1/4 + 1/9 + ... + 1/
n2 + ... = π
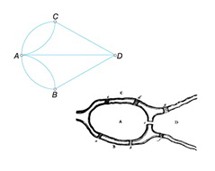
2/6. Przedstawione przez niego w pracy z 1736 zadanie zwane problem mostów królewieckich zapoczątkowało teorię grafów.
Do najważniejszych osiągnięć Eulera w dziedzinie fizyki należą: pierwsze poprawne sformułowanie zasady najmniejszego działania Maupertuisa (zasada wariacyjna, 1744), wprowadzenie w mechanice płynów prawa niezależności ciśnienia od orientacji elementu powierzchniowego (1755), podanie podstawowego równania mechaniki analitycznej — równania płynu doskonałego. Analizował również problem drgającej struny (1748). W 1765 podał równania dynamiczne i kinematyczne opisujące ruch bryły sztywnej (równania ruchu obrotowego Eulera, 1765).
Oprócz matematyki i fizyki jego prace dotyczyły również: teorii nawigacji, teorii muzyki, przypływów i odpływów morza, ruchów planet i komet, balistyki, dioptryki i wielu innych. Był jednym z najbardziej płodnych matematyków w historii: w sumie był autorem ok. 900 prac — edycja Opera omnia, dotąd nie ukończona, jest wydawana od 1911 (ukazało się ponad 70 tomów).
 , ur. 15 IV 1707, Bazylea, zm. 18 IX 1783, Petersburg,
, ur. 15 IV 1707, Bazylea, zm. 18 IX 1783, Petersburg,
 , ur. 15 IV 1707, Bazylea, zm. 18 IX 1783, Petersburg,
, ur. 15 IV 1707, Bazylea, zm. 18 IX 1783, Petersburg,
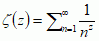 (co uznaje się za początek analitycznej teorii liczb), udowodnił istnienie pierwiastków pierwotnych liczb pierwszych, sformułował prawo wzajemności reszt kwadratowych i rozstrzygnął wiele problemów postawionych przez P. Fermata. Odkrył wieloznaczność logarytmu zespolonego, wprowadził do dziś używane symbole dla liczb: i, e, oraz udowodnił związek 1+eiπ = 0, zachodzący między nimi. Odkrył też wiele innych wzorów matematycznych, z których najsławniejszy to: 1 + 1/4 + 1/9 + ... + 1/n2 + ... = π2/6. Przedstawione przez niego w pracy z 1736 zadanie zwane problem mostów królewieckich zapoczątkowało teorię grafów.
(co uznaje się za początek analitycznej teorii liczb), udowodnił istnienie pierwiastków pierwotnych liczb pierwszych, sformułował prawo wzajemności reszt kwadratowych i rozstrzygnął wiele problemów postawionych przez P. Fermata. Odkrył wieloznaczność logarytmu zespolonego, wprowadził do dziś używane symbole dla liczb: i, e, oraz udowodnił związek 1+eiπ = 0, zachodzący między nimi. Odkrył też wiele innych wzorów matematycznych, z których najsławniejszy to: 1 + 1/4 + 1/9 + ... + 1/n2 + ... = π2/6. Przedstawione przez niego w pracy z 1736 zadanie zwane problem mostów królewieckich zapoczątkowało teorię grafów.