funkcje trygonometryczne

funkcje trygonometryczne,

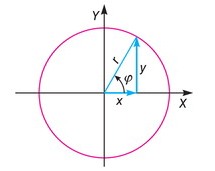
mat. funkcje kąta φ, oznaczane symbolami: sinφ (sinus), cosφ (cosinus), tgφ (tangens), ctgφ (cotangens), secφ (secans), cosecφ (cosecans), określone za pomocą wzorów: sinφ = y/r, cosφ = x/r, tgφ = y/x = sinφ/cosφ (dla kątów φ ≠ π/2 ± nπ, gdzie n = 0, 1, 2, 3, ...), ctgφ = x/y = cosφ/sinφ (dla φ ≠ ±nπ), secφ = r/x = 1/cosφ (dla φ ≠ π/2 ± nπ), cosecφ = r/y = 1/sinφ (dla φ ≠ ±nπ).

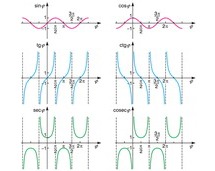
Funkcje trygonometryczne są funkcjami okresowymi, mianowicie sin, cos, sec, cosec mają okres 360° (= 2π rad), a tg i ctg — okres 180° (= π rad). W tablicach matematycznych są podane wartości liczbowe funkcji trygonometrycznych dla kątów leżących w pierwszej ćwiartce, tzn. 0 < φ < 90° (niekiedy tylko dla kątów 0 < φ < 45°); w celu znalezienia wartości funkcji trygonometrycznych dla dużych kątów stosuje się tzw. wzory redukcyjne:

sin(φ + kπ) = (–1)^k sinφ, cos(φ + kπ) = (–1)^k cosφ, tg(φ + kπ) = tgφ, gdzie k — dowolna liczba całkowita, sin(φ + π/2) = cosφ, cos(φ + π/2) = –sinφ, tg(φ + π/2) = –ctgφ.

Funkcje trygonometryczne spełniają wiele tożsamości, z których oprócz podstawowej relacji cos²φ + sin²φ = 1, najważniejsze to:

1) wzory wyrażające funkcję trygonometryczną sumy lub różnicy kątów w zależności od funkcji trygonometrycznych poszczególnych kątów:

sin(α ± β) = sinα · cosβ ± cosα · sinβ,

cos(α ± β) = cosα · cosβ ± sinα · sinβ,

tg(α ± β) = (tgα ± tgβ)/(1 ± tgα · tgβ),

przy czym znaki plus i minus górne (dolne) po lewej stronie odpowiadają znakom górnym (dolnym) po prawej stronie tych wzorów;

2) wzory na sumę lub różnicę funkcji trygonometrycznych (Regiomontanus, XV w.; J. Napier, XVII w.):

sinα ± sinβ = 2sin¹/₂(α ± β) · cos¹/₂(α ± β),

tgα ± tgβ = [sin(α ± β)]/(cosα · cosβ),

cosα + cosβ = 2cos¹/₂(α + β) · cos¹/₂(α – β),

cosα – cosβ = –2sin¹/₂(α + β) · sin¹/₂(α – β);

3) wzory na iloczyny funkcji trygonometrycznych kątów:

sinα · cosβ = ¹/₂[sin(α + β) + sin(α – β)],

sinα · sinβ = ¹/₂[cos(α – β) – cos(α + β)],

cosα · cosβ = ¹/₂[cos(α + β) + cos(α – β)];

4) wzory wyrażające funkcje trygonometryczne przez szeregi potęgowe (I. Newton, 1669), np.:

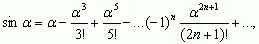
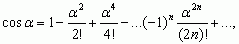
zbieżne dla każdej wartości kąta α (wyrażonej w radianach);

5) wzory na pochodne funkcji trygonometrycznych (różniczkowy rachunek) i na całki funkcji trygonometrycznych (całkowy rachunek).

W analizie matematycznej funkcji trygonometrycznych sin i cos definiuje się analitycznie (nie geometrycznie) za pomocą ostatnich dwóch szeregów potęgowych, które służą także jako definicje sinusa i cosinusa dla zespolonych wartości argumentów:

,

,

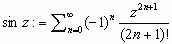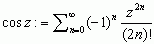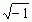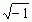gdzie z = x + i y (i = ; x, y — liczby rzeczywiste); funkcje trygonometryczne argumentu zespolonego związane są z funkcją wykładniczą e^z wzorami Eulera. Funkcje trygonometryczne argumentu zespolonego mogą przybierać wartości rzeczywiste większe niż 1. Funkcje odwrotne do funkcji trygonometrycznych nazywają się funkcjami kołowymi lub cyklometrycznymi.

Pierwsze pojęcia dotyczące funkcji trygonometrycznych sięgają czasów starożytnej Grecji (Euklides, Archimedes, Apoloniusz z Pergi i in.); pierwszą tablicę sinusów zestawił Klaudiusz Ptolemeusz (II w.); funkcje tg α i ctg α pojawiają się u Al-Battaniego (IX–X w.) i u Abu al-Wafy (X w.); ten ostatni stosował również funkcje trygonometryczne secα i cosecα; Arjabhata znał tożsamość cos²α + sin²α = 1. Współczesna postać funkcji trygonometrycznych jest zasługą L. Eulera (XVIII w.); wprowadził on definicję funkcji trygonometrycznych dla argumentów zespolonych, odkrył związek funkcji trygonometrycznych z funkcją wykładniczą e^z, wykazał ortogonalność układu funkcji 1, cosα, sinα, cos2α, sin2α, ... , uzyskał rozwinięcie sinusa i cosinusa w iloczyny nieskończone, jak również rozkład cotangensa i tangensa na ułamki proste. Funkcje trygonometryczne stosuje się szeroko przy badaniu zjawisk okresowych (periodycznych), np. drgań prętów, strun.

Trygonometryczne koło

Trygonometryczne funkcje