różniczkowy rachunek,
mat.
różniczkowy rachunek
Encyklopedia PWN
dział analizy matematycznej poświęcony badaniu własności pochodnych funkcji i różniczek, technice obliczania pochodnych i ich zastosowaniom; wraz z rachunkiem całkowym oraz równaniami różniczkowymi (zwyczajnymi i cząstkowymi) i całkowymi stanowi aparat badawczy szeroko stosowany w naukach przyrodniczych, technice, ekonomii. Podstawowym pojęciem rachunku różniczkowego jest pochodna funkcji; podstawowe reguły obliczania pochodnych opierają się na następujących wzorach (pochodna oznaczona jest primem: y′ = dy/dx):
a) [f(x) ± g(x)]′ = f′(x) ± g′(x);
b) [f(x) · g(x)]′ = f′(x) · g (x) + f(x) · g′(x);
c) [c · f(x)]′ = c · f′(x), c = const;
d) 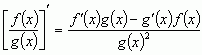 , g(x) ≠ 0;
, g(x) ≠ 0;
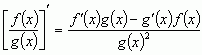 , g(x) ≠ 0;
, g(x) ≠ 0; e) 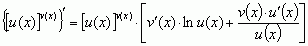 ;
;
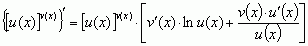 ;
; f) wzór na pochodną funkcji złożonej: jeżeli y = f(u) oraz u = φ(x), to pochodna funkcji złożonej y = g(x) = f[φ(x)] jest równa dy/dx = dy/du · du/dx = f′(u) · φ′(x) = f′[φ(x)] · φ′(x);
g) wzór na pochodną funkcji odwrotnej: jeżeli funkcja x = φ(y) ma funkcję odwrotną y = f(x), to pochodna funkcji odwrotnej wyraża się wzorem 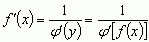 lub krócej
lub krócej 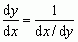 .
.
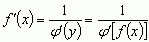 lub krócej
lub krócej 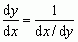 .
. Łącząc powyższe reguły z pewnymi podstawowymi wzorami na pochodne funkcji elementarnych (np. (xn)′ = nxn – 1, (logax)′ = 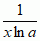 , (sin x)′ = cos x, (cos x)′ = –sin x, (arc sin x)′ = 1/
, (sin x)′ = cos x, (cos x)′ = –sin x, (arc sin x)′ = 1/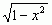 , (arc cos x)′ = –1/
, (arc cos x)′ = –1/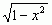 , (ax)′ = ax · ln a), można obliczać pochodne dość szerokiej klasy funkcji.
, (ax)′ = ax · ln a), można obliczać pochodne dość szerokiej klasy funkcji.
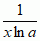 , (sin x)′ = cos x, (cos x)′ = –sin x, (arc sin x)′ = 1/
, (sin x)′ = cos x, (cos x)′ = –sin x, (arc sin x)′ = 1/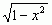 , (arc cos x)′ = –1/
, (arc cos x)′ = –1/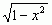 , (ax)′ = ax · ln a), można obliczać pochodne dość szerokiej klasy funkcji.
, (ax)′ = ax · ln a), można obliczać pochodne dość szerokiej klasy funkcji. Początki rachunku różniczkowego przypadają na 2. połowę XVII w.; twórcami rachunku różniczkowego są I. Newton i G.W. Leibniz, przy czym punktem wyjścia dla Newtona były zagadnienia dynamiki ciał (wyprowadził on pochodną jako prędkość ciała); dla Leibniza punktem wyjścia były zagadnienia natury geometrycznej, przede wszystkim zagadnienie definicji stycznej do krzywej; Leibniz wprowadził wiele pojęć rachunku różniczkowego (różniczka, pochodna cząstkowa), jak też wiele wygodnych oznaczeń (∂ — oznaczenie różniczki, ∂y/∂x — pochodnej), które zachowały się w matematyce; pierwszy podręcznik rachunku różniczkowego opublikował 1696 G.F.A. de L’Hospital Analyse des infiniment petits pour l’intelligence des lignes courbes; olbrzymi wkład w rozwój rachunku różniczkowego wniósł L. Euler, pisząc m.in. 2 klasyczne podręczniki rachunku różniczkowego (1748 i 1755), które stały się wzorem późniejszych podręczników z tego zakresu; reforma analizy matematycznej, a w szczególności rachunku różniczkowego, była w XIX w. głównie dziełem A.L. Cauchy’ego, B. Bolzana, C.F. Gaussa i K. Weierstrassa (ugruntowanie precyzyjnej teorii granic).


