pochodna funkcji,
mat. tempo zmian wartości funkcji;
- granica
- funkcja
- analiza matematyczna
- rachunek różniczkowy i całkowy
- funkcja liniowa
- Darboux własność
- ekstremum funkcji
- pochodna cząstkowa
- funkcje analityczne
- szereg
- rozmaitość
- hiperpowierzchnia
- przestrzeń Banacha
- całka
- całkowanie
- iloraz różnicowy
- normalna
- funkcja pierwotna
- równanie różnicowe
- różniczkowanie
- różniczkowy rachunek
- zbieżność

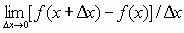 , to granicę tę nazywa się pochodną funkcji f(x) w punkcie x i oznacza symbolem f ′(x) lub df(x)/dx; wyrażenie [f(x + Δx) – f(x)]/Δx nazywa się przy tym
, to granicę tę nazywa się pochodną funkcji f(x) w punkcie x i oznacza symbolem f ′(x) lub df(x)/dx; wyrażenie [f(x + Δx) – f(x)]/Δx nazywa się przy tym 
