szereg,
mat. jedno z najważniejszych pojęć analizy matematycznej, pozwalające w pewnych sytuacjach nadać ścisły sens dodawaniu nieskończonej liczby składników;
- szereg potęgowy
- szereg Taylora
- szereg trygonometryczny
- przestrzeń liniowa
- ciąg
- granica
- funkcja dzeta (zeta) Riemanna
- bijekcja
- wartość bezwzględna
- liczby zespolone
- norma
- przestrzeń Banacha
- funkcje analityczne
- szereg Fouriera
- całkowanie
- funkcja
- szereg Leibniza
- majoranta
- minoranta
- mnożenie
- pochodna funkcji
- rachunek różniczkowy i całkowy
- rozwinięcie funkcji w szereg
- suma nieskończona
- suma szeregu
- zbieżność

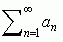 ; jeżeli poszczególne składniki (wyrazy) szeregu an są liczbami (rzeczywistymi lub zespolonymi), mówi się o szeregu liczbowym, jeżeli zaś są funkcjami — o szeregu funkcyjnym; suma Sn = a1 + a2 + ... + an nazywa się n-tą sumą częściową szeregu. Szereg liczbowy jest
; jeżeli poszczególne składniki (wyrazy) szeregu an są liczbami (rzeczywistymi lub zespolonymi), mówi się o szeregu liczbowym, jeżeli zaś są funkcjami — o szeregu funkcyjnym; suma Sn = a1 + a2 + ... + an nazywa się n-tą sumą częściową szeregu. Szereg liczbowy jest 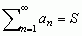 ; szereg liczbowy, który nie jest zbieżny, nazywa się
; szereg liczbowy, który nie jest zbieżny, nazywa się 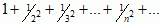 jest zbieżny do liczby π2/6. Szereg funkcyjny
jest zbieżny do liczby π2/6. Szereg funkcyjny 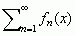 jest zbieżny do funkcji f(x), gdy ciąg sum częściowych Sn(x) = f1(x) + f2(x) + ... + fn(x) jest zbieżny do funkcji granicznej f(x); do najważniejszych szeregów funkcyjnych należą
jest zbieżny do funkcji f(x), gdy ciąg sum częściowych Sn(x) = f1(x) + f2(x) + ... + fn(x) jest zbieżny do funkcji granicznej f(x); do najważniejszych szeregów funkcyjnych należą 
