rozwinięcie funkcji w szereg

rozwinięcie funkcji w szereg,

mat. przedstawienie danej funkcji f — o wartościach rzeczywistych bądź zespolonych, lub ogólniej, o wartościach z przestrzeni wektorowej unormowanej (przestrzeń unormowana), np. n-wymiarowej przestrzeni kartezjańskiej, przestrzeni Banacha, przestrzeni Hilberta — w postaci sumy szeregu funkcyjnego (szereg): f(x) = 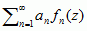, gdzie a_n są współczynnikami, f_n zaś funkcjami, na ogół prostszej natury niż sama funkcja f;

lub szeregu Maclaurina (w otoczeniu zera):

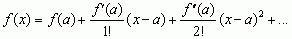
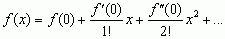f(x) = f(0) + ...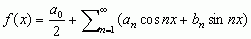

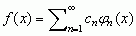lub szeregu Fouriera (dla funkcji okresowej o okresie 2π):

lub ogólnie, za pomocą szeregu względem pewnego ortonormalnego układu funkcji φ₁(x), φ₂(x), ... , φ_n(x):

, gdzie współczynniki rozwinięcia c_n wyrażają się wzorami 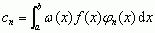, przy czym funkcja ω(x) jest dana i nazywa się wagą.