falka

falka, ang. wavelet, fr. ondelette,

mat. ważne i użyteczne narzędzie współcz. matematyki stosowanej: funkcja Ψ zmiennej rzeczywistej nazywa się f. (lub matką-f.), gdy rodzina funkcji uzyskanych z niej poprzez skalowanie i przesuwanie Ψ_n,k(x) = 2^–n/2Ψ(2ⁿx – k), gdzie n i k — liczby całkowite, stanowi bazę ortonormalną przestrzeni L²(ℝ) funkcji całkowalnych z kwadratem na osi rzeczywistej, tzn. gdy dowolną funkcję f(x) z przestrzeni L²(ℝ) można przedstawić w postaci szeregu f.: f(x) = 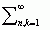a_{n, k}Ψ_{n, k}(x).

Intensywny rozwój teorii f. nastąpił w 1. poł. lat 80. XX w. (R. Coifman, I. Daubechies, A. Grosmann, S. Mallat, Y. Meyer, J. Morlet), gł. ze względu na liczne zastosowania f. w kodowaniu i przetwarzaniu sygnałów — oszczędnym kodowaniu bardzo dużych baz danych (np. bazy FBI z odciskami palców kilku mln osób) oraz filtrowaniu sygnału niosącego informację z szumów i zakłóceń. W tego typu zastosowaniach f. są z reguły użyteczniejsze od szeroko wykorzystywanych szeregów Fouriera.