pakiet falkowy,
mat., telekom. funkcja dobrze zlokalizowana w dziedzinie zmiennej niezależnej, np. w dziedzinie czasu t, i w dziedzinie transformaty Fouriera (Fouriera przekształcenie), tj. w dziedzinie częst. f.
pakiet falkowy
Encyklopedia PWN
Dobra lokalizacja funkcji w dziedzinie zmiennej niezależnej oznacza, że poza pewnym skończonym przedziałem jest ona wszędzie równa zeru albo szybko, np. wykładniczo, zanika; dobra lokalizacja w dziedzinie częst. oznacza, że poza pewnym skończonym przedziałem częst. moduł transformaty Fouriera funkcji jest wszędzie równy zeru albo szybko zanika. P.f. są gł. wykorzystywane w analizie sygnałów. Tworzą rodziny dwuparametrowych funkcji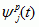 
, gdzie j ≥ 0 i 0 ≤ p < 2 j; pakietem 
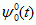jest funkcja skalująca (analiza wielorozdzielcza), a pozostałe p.f. są obliczane rekurencyjnie (rekurencyjny wzór). Z każdego p.f. mogą być utworzone 2 nowe p.f., przy czym energia jednego z nich jest skupiona w dolnej połowie, a drugiego — w górnej połowie pasma częstotliwości p.f., z którego powstały. Zbiory p.f. tworzą bazy do aproksymacji sygnałów. W analizie sygnału f(t) za pomocą p.f. otrzymuje się rozwinięcie sygnału w postaci następującej sumy:
.
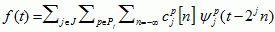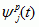, gdzie j ≥ 0 i 0 ≤ p < 2 j; pakietem 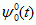jest funkcja skalująca (analiza wielorozdzielcza), a pozostałe p.f. są obliczane rekurencyjnie (rekurencyjny wzór). Z każdego p.f. mogą być utworzone 2 nowe p.f., przy czym energia jednego z nich jest skupiona w dolnej połowie, a drugiego — w górnej połowie pasma częstotliwości p.f., z którego powstały. Zbiory p.f. tworzą bazy do aproksymacji sygnałów. W analizie sygnału f(t) za pomocą p.f. otrzymuje się rozwinięcie sygnału w postaci następującej sumy: 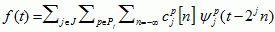. Współczynniki rozwinięcia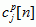 
, tj. współczynniki wagowe przy poszczególnych p.f. sumy, oblicza się za pomocą transformacji falkowej sygnału (transformata falkowa); zbiór indeksów J i zbiory indeksów PJ zależą od wyboru p.f. do aproksymacji; np. wybierając p.f.: 
, 
, 
, 
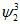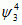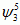, otrzymuje się: J = {1, 2, 3}, P1 = {0}, P2 = {3}, P3 = {4, 5}.
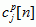, tj. współczynniki wagowe przy poszczególnych p.f. sumy, oblicza się za pomocą transformacji falkowej sygnału (transformata falkowa); zbiór indeksów J i zbiory indeksów PJ zależą od wyboru p.f. do aproksymacji; np. wybierając p.f.: , , 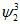, , 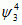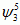otrzymuje się: J = {1, 2, 3}, P1 = {0}, P2 = {3}, P3 = {4, 5}. Wybór właściwych p.f. umożliwia przedstawienie sygnału w sposób pokazujący jego właściwości czasowo-częstotliwościowe; pozwala zwłaszcza na analizę sygnałów niestacjonarnych oraz przedstawianie zmian ich właściwości czasowo-częstotliwościowych. Możliwe jest poszukiwanie najlepszej, wg przyjętego kryterium, bazy p.f. dla analizowanego sygnału. Przedstawienie sygnału za pomocą p.f. jest szczególnie przydatne w kompresji (kompresja danych) i odszumianiu sygnału. P.f. znalazły zastosowanie m.in. w kompresji dźwięku i obrazu oraz w analizie sygnałów sejsmicznych i biomedycznych.
Waldemar Rakowski
