Fouriera przekształcenie, transformacja Fouriera,
mat. przyporządkowanie (transformacja), w którym danej funkcji f(x) odpowiada funkcja F(λ) = 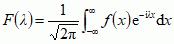 (1) (czynnik 1/
(1) (czynnik 1/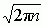 jest przez niektórych autorów włączany do f(x), i — jednostka urojona);
jest przez niektórych autorów włączany do f(x), i — jednostka urojona);
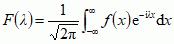 (1) (czynnik 1/
(1) (czynnik 1/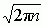 jest przez niektórych autorów włączany do f(x), i — jednostka urojona);
jest przez niektórych autorów włączany do f(x), i — jednostka urojona);
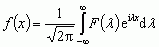 (2)
(2) 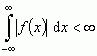 lub
lub 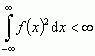 .
.