funkcja charakterystyczna zmiennej losowej,
mat. funkcja związana ze zmienną losową X wzorem φ(t) = E(eitX), gdzie t jest liczbą rzeczywistą, a E oznacza wartość oczekiwaną;
funkcja charakterystyczna zmiennej losowej
Encyklopedia PWN
dla zmiennej losowej typu ciągłego funkcja charakterystyczna zmiennej losowej jest transformatą Fouriera (Fouriera przekształcenie) jej gęstości rozkładu f, czyli wyraża się wzorem φ(t) = 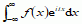 ; za pomocą funkcji charakterystycznej zmiennej losowej można łatwo obliczyć momenty zmiennej losowej; funkcja charakterystyczna zmiennej losowej sumy skończonej liczby niezależnych zmiennych losowych jest iloczynem funkcji charakterystycznej zmiennej losowej każdej z tych zmiennych; funkcja charakterystyczna zmiennej losowej wyznacza jednoznacznie dystrybuantę zmiennej losowej; własności funkcji charakterystycznej zmiennej losowej wykorzystuje się m.in. w dowodach twierdzeń granicznych.
; za pomocą funkcji charakterystycznej zmiennej losowej można łatwo obliczyć momenty zmiennej losowej; funkcja charakterystyczna zmiennej losowej sumy skończonej liczby niezależnych zmiennych losowych jest iloczynem funkcji charakterystycznej zmiennej losowej każdej z tych zmiennych; funkcja charakterystyczna zmiennej losowej wyznacza jednoznacznie dystrybuantę zmiennej losowej; własności funkcji charakterystycznej zmiennej losowej wykorzystuje się m.in. w dowodach twierdzeń granicznych.
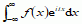 ; za pomocą funkcji charakterystycznej zmiennej losowej można łatwo obliczyć momenty zmiennej losowej; funkcja charakterystyczna zmiennej losowej sumy skończonej liczby niezależnych zmiennych losowych jest iloczynem funkcji charakterystycznej zmiennej losowej każdej z tych zmiennych; funkcja charakterystyczna zmiennej losowej wyznacza jednoznacznie dystrybuantę zmiennej losowej; własności funkcji charakterystycznej zmiennej losowej wykorzystuje się m.in. w dowodach twierdzeń granicznych.
; za pomocą funkcji charakterystycznej zmiennej losowej można łatwo obliczyć momenty zmiennej losowej; funkcja charakterystyczna zmiennej losowej sumy skończonej liczby niezależnych zmiennych losowych jest iloczynem funkcji charakterystycznej zmiennej losowej każdej z tych zmiennych; funkcja charakterystyczna zmiennej losowej wyznacza jednoznacznie dystrybuantę zmiennej losowej; własności funkcji charakterystycznej zmiennej losowej wykorzystuje się m.in. w dowodach twierdzeń granicznych. 

