Laplace’a przekształcenie

Laplace’a przekształcenie, transformacja Laplace’a,

mat. przekształcenie całkowe, które funkcji zmiennej rzeczywistej f(t) przyporządkowuje funkcję zmiennej zespolonej F(z): 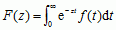, gdzie f(t) jest funkcją określoną na półprostej (0, +∞) — p.L. jednostronne, lub 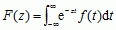, gdzie f(t) jest określona na całej prostej (tzn. −∞ < t < +∞) — p.L. dwustronne.

Podstawiając z = ix, gdzie i = , otrzymuje się z dwustronnego p.L. przekształcenie Fouriera. Obszar określoności (czyli dziedzina) funkcji F(z) jest zawsze półpłaszczyzną postaci Re z > a (symbol Re z oznacza część rzeczywistą liczby z). P.L. oznacza się zwykle literą ℒ: F(z) = ℒ[f(t)]. Dla p.L. zachodzą następujące zależności: ℒ[f₁ ∗ f₂] = ℒ[f₁] · ℒ[f₂], gdzie f₁ ∗ f₂ oznacza splot funkcji f₁ i f₂, oraz ℒ[f'(t)] = zℒ[f(t)] − f(0). Ta ostatnia własność p.L. pozwoliła na zastosowanie tego przekształcenia do rachunku operatorowego w celu rozwiązywania równań różniczkowych zwyczajnych o stałych współczynnikach. Przy pewnych założeniach dotyczących funkcji f p.L. 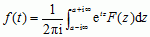ma transformację odwrotną postaci , gdzie całkowanie odbywa się wzdłuż prostej Re z = a, równoległej do osi urojonej, położonej w obszarze określoności funkcji F(z). Całka 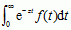była szczegółowo badana przez P.S. de Laplace’a w dziele o teorii prawdopodobieństwa (1812).