operatorowy rachunek,
mat. dział matematyki obejmujący metody rozwiązywania niektórych typów równań różniczkowych, a także różniczkowo-całkowych, polegające na algebraizacji rozwiązywanego równania lub układu równań;
operatorowy rachunek
Encyklopedia PWN
największe znaczenie uzyskał rachunek operatorowy jako prosta, a jednocześnie ogólna metoda rozwiązywania liniowych równań różniczkowych zwyczajnych o stałych współczynnikach oraz układów takich równań; rachunek operatorowy znalazł szerokie zastosowanie w elektrotechnice, automatyce, mechanice itp.; wśród metod operatorowych największe znaczenie mają te, które są oparte na przekształceniach całkowych Laplace’a i Fouriera; przekształcenie Laplace’a przyporządkowuje funkcji f(t) określonej w przedziale (0, +∞) funkcję F(s) zw. transformatą funkcji f(t) (s — zmienna zespolona) wg wzoru: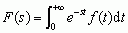 
lub w skrócie F(s) = £[f(t)]; przy pewnych założeniach dodatkowych można — na odwrót — wyrazić funkcję f(t) przez jej transformatę F(s), mianowicie f(t) = £–1[F(s)] =
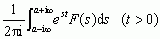; podobnie wzór £[f (n)(t)] = snF(s) –
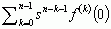uzależnia transformatę n-tej pochodnej f (n)(t) od transformaty F(s) samej funkcji f(t); na przykład, w celu rozwiązania równania różniczkowego x″(t) + x′(t) = 1 z warunkami początkowymi: x(0) = 0, x′(0) = –1, mnoży się obie strony rozważanego równania różniczkowego przez e–st i całkuje w granicach od 0 do +∞, czyli poddaje się to równanie przekształceniu Laplace’a; oznaczając X(s) = £[x(t)] oraz uwzględniając, że £[1] = 1/s, otrzymuje się równanie algebraiczne s2X(s) + 1 + sX(s) = 1/s, w którym niewiadomą jest transformata X(s) szukanej funkcji x(t); otrzymuje się X(s) = (1 – s)/[s2(1 + s)]; wreszcie wykonuje się odwrotne przekształcenie Laplace’a:
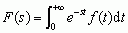lub w skrócie F(s) = £[f(t)]; przy pewnych założeniach dodatkowych można — na odwrót — wyrazić funkcję f(t) przez jej transformatę F(s), mianowicie f(t) = £–1[F(s)] =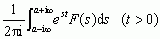; podobnie wzór £[f (n)(t)] = snF(s) – 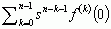uzależnia transformatę n-tej pochodnej f (n)(t) od transformaty F(s) samej funkcji f(t); na przykład, w celu rozwiązania równania różniczkowego x″(t) + x′(t) = 1 z warunkami początkowymi: x(0) = 0, x′(0) = –1, mnoży się obie strony rozważanego równania różniczkowego przez e–st i całkuje w granicach od 0 do +∞, czyli poddaje się to równanie przekształceniu Laplace’a; oznaczając X(s) = £[x(t)] oraz uwzględniając, że £[1] = 1/s, otrzymuje się równanie algebraiczne s2X(s) + 1 + sX(s) = 1/s, w którym niewiadomą jest transformata X(s) szukanej funkcji x(t); otrzymuje się X(s) = (1 – s)/[s2(1 + s)]; wreszcie wykonuje się odwrotne przekształcenie Laplace’a:
x(t) = £–1[X(s)] = £–1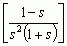
= t – 2 + 2e–t
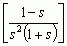= t – 2 + 2e–t i otrzymuje rozwiązanie rozważanego równania różniczkowego spełniające zał. warunki początkowe. Za twórcę rachunku operatorowego jest uważany O. Heaviside (Electrical Papers 1892); 1950 J. Mikusiński podał nowe podstawy rachunku operatorowego wprowadzając nowy typ operatorów, zw. obecnie operatorami Mikusińskiego.
Znaleziono w książkach Grupy PWN
Trwa wyszukiwanie... 
