Fouriera szybka transformata, ang. Fast Fourier Transform (FFT),
mat. bardzo efektywny (jak się przypuszcza optymalny) algorytm obliczania dyskretnej transformaty Fouriera (Fouriera przekształcenie), powszechnie wykorzystywany w wielu zagadnieniach numerycznych, np. do mnożenia macierzy i wielomianów, a także znajdowania przybliżonych rozwiązań równań różniczkowych.
Fouriera szybka transformata
Encyklopedia PWN
Znajdowanie dyskretnej transformaty Fouriera ciągu (a0, a1,... , an –1) polega na obliczeniu wartości wielomianu p(x) = Σ ajxj we wszystkich pierwiastkach stopnia n z jedynki, tzn. w punktach x postaci ωj = e2πi j/n, gdzie i =  , a j = 0, 1,... , n – 1; jest to równoważne obliczeniu reszt z dzielenia wielomianu p(x) przez każdy z dwumianów x – ωj. Zasadniczy pomysł algorytmu szybkiej transformaty Fouriera, pochodzący jeszcze od C.F. Gaussa, polega na tym, by dla n = 2k obliczać owe reszty rekurencyjnie, dzieląc wielomian przez takie iloczyny dwumianów x –ωj, których stopnie też są potęgami dwójki, przy czym punkty ωj porządkuje się w taki sposób, by wszystkie te iloczyny miały postać
, a j = 0, 1,... , n – 1; jest to równoważne obliczeniu reszt z dzielenia wielomianu p(x) przez każdy z dwumianów x – ωj. Zasadniczy pomysł algorytmu szybkiej transformaty Fouriera, pochodzący jeszcze od C.F. Gaussa, polega na tym, by dla n = 2k obliczać owe reszty rekurencyjnie, dzieląc wielomian przez takie iloczyny dwumianów x –ωj, których stopnie też są potęgami dwójki, przy czym punkty ωj porządkuje się w taki sposób, by wszystkie te iloczyny miały postać 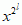 – ωj, co niesłychanie upraszcza dzielenie; na początku dzieli się wielomian p(x) stopnia n – 1 przez dwa wielomiany stopnia n/2, następnie każdą z obliczonych reszt dzieli się przez dwa wielomiany stopnia n/4 itd. Algorytm mnożenia dwóch wielomianów stopnia n oparty na szybkiej transformacie Fouriera wymaga co najwyżej const · n logn operacji arytmetycznych — dla porównania, klasyczny algorytm mnożenia wielomianów stopnia n wymaga const · n2 operacji, jest więc znacznie kosztowniejszy.
– ωj, co niesłychanie upraszcza dzielenie; na początku dzieli się wielomian p(x) stopnia n – 1 przez dwa wielomiany stopnia n/2, następnie każdą z obliczonych reszt dzieli się przez dwa wielomiany stopnia n/4 itd. Algorytm mnożenia dwóch wielomianów stopnia n oparty na szybkiej transformacie Fouriera wymaga co najwyżej const · n logn operacji arytmetycznych — dla porównania, klasyczny algorytm mnożenia wielomianów stopnia n wymaga const · n2 operacji, jest więc znacznie kosztowniejszy.
 , a j = 0, 1,... , n – 1; jest to równoważne obliczeniu reszt z dzielenia wielomianu p(x) przez każdy z dwumianów x – ωj. Zasadniczy pomysł algorytmu szybkiej transformaty Fouriera, pochodzący jeszcze od C.F. Gaussa, polega na tym, by dla n = 2k obliczać owe reszty rekurencyjnie, dzieląc wielomian przez takie iloczyny dwumianów x –ωj, których stopnie też są potęgami dwójki, przy czym punkty ωj porządkuje się w taki sposób, by wszystkie te iloczyny miały postać
, a j = 0, 1,... , n – 1; jest to równoważne obliczeniu reszt z dzielenia wielomianu p(x) przez każdy z dwumianów x – ωj. Zasadniczy pomysł algorytmu szybkiej transformaty Fouriera, pochodzący jeszcze od C.F. Gaussa, polega na tym, by dla n = 2k obliczać owe reszty rekurencyjnie, dzieląc wielomian przez takie iloczyny dwumianów x –ωj, których stopnie też są potęgami dwójki, przy czym punkty ωj porządkuje się w taki sposób, by wszystkie te iloczyny miały postać 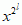 – ωj, co niesłychanie upraszcza dzielenie; na początku dzieli się wielomian p(x) stopnia n – 1 przez dwa wielomiany stopnia n/2, następnie każdą z obliczonych reszt dzieli się przez dwa wielomiany stopnia n/4 itd. Algorytm mnożenia dwóch wielomianów stopnia n oparty na szybkiej transformacie Fouriera wymaga co najwyżej const · n logn operacji arytmetycznych — dla porównania, klasyczny algorytm mnożenia wielomianów stopnia n wymaga const · n2 operacji, jest więc znacznie kosztowniejszy.
– ωj, co niesłychanie upraszcza dzielenie; na początku dzieli się wielomian p(x) stopnia n – 1 przez dwa wielomiany stopnia n/2, następnie każdą z obliczonych reszt dzieli się przez dwa wielomiany stopnia n/4 itd. Algorytm mnożenia dwóch wielomianów stopnia n oparty na szybkiej transformacie Fouriera wymaga co najwyżej const · n logn operacji arytmetycznych — dla porównania, klasyczny algorytm mnożenia wielomianów stopnia n wymaga const · n2 operacji, jest więc znacznie kosztowniejszy.


