widmo sygnału, widmo przebiegu wielkości,
rozkład wartości określonej wielkości fizycznej charakteryzującej sygnał w zależności od jego częstotliwości;
widmo sygnału
Encyklopedia PWN
powstaje w wyniku operacji matematycznej polegającej na rozłożeniu sygnału na składowe przebiegi harmoniczne o różnych częstotliwościach. Widmo stanowi więc reprezentację częstotliwościową sygnału, a jego przebieg — reprezentację czasową.
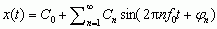 ,
,
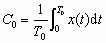 ,
, 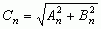 ,
,
 , w której funkcja
, w której funkcja 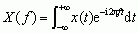 stanowi transformatę Fouriera i przedstawia właśnie widmo gęstości amplitudy nieokresowego przebiegu czasowego x(t).
stanowi transformatę Fouriera i przedstawia właśnie widmo gęstości amplitudy nieokresowego przebiegu czasowego x(t).
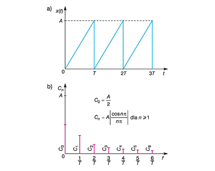
Z teorii przekształcenia Fouriera wynika, że jeżeli sygnał jest okresową funkcją czasu o okresie T0: x(t) = x(t + kT0), gdzie k jest liczbą całkowitą, to można go rozwinąć w szereg Fouriera
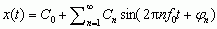 ,
, gdzie f0 = 1/T0 — częstotliwość podstawowa. Sygnał można więc przedstawić jako sumę składowej stałej (przebiegu niezależnego od czasu) o amplitudzie C0 i przebiegów sinusoidalnych (drgań harmonicznych) o amplitudach Cn, częstotliwościach f0n i fazach początkowych φn; sygnałowi okresowemu odpowiada zatem widmo prążkowe (dyskretne), mogące zawierać tylko składniki Cn (prążki) o dyskretnych wartościach częstotliwości, równych całkowitej wielokrotności częstotliwości podstawowej f0 = 1/T0.
Wartości współczynników C0, Cn i φn można wyznaczyć z następujących zależności:
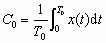 ,
, 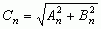 ,
,
φn = arc tg(Bn/An), gdzie 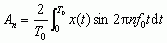 ,
, 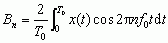 .
.
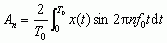 ,
, 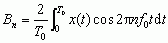 .
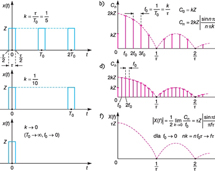
.Na rysunku zestawiono przebiegi czasowe i widma amplitudy sygnałów impulsowych o różnym współczynniku wypełnienia k = τ/T (τ — czas trwania pojedynczego impulsu). Wraz ze zmniejszaniem się k, tj. zwiększaniem T przy stałym τ, składowe harmoniczne (prążki) w widmie leżą coraz bliżej siebie, a ich amplitudy (wysokości prążków) stopniowo maleją. W granicznym przypadku, gdy k maleje do zera (T rośnie do nieskończoności), amplitudy prążków i odległości między prążkami stają się nieskończenie małe, a widmo z prążkowego przechodzi w ciągłe. Odpowiada to pojedynczemu impulsowi (sygnałowi nieokresowemu). Wprowadza się wówczas pojęcie widma gęstości amplitudy, które jest określone funkcją 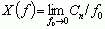 , a zamiast szeregu Fouriera stosuje się całkę Fouriera:
, a zamiast szeregu Fouriera stosuje się całkę Fouriera:
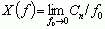 , a zamiast szeregu Fouriera stosuje się całkę Fouriera:
, a zamiast szeregu Fouriera stosuje się całkę Fouriera: , w której funkcja
, w której funkcja 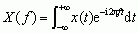 stanowi transformatę Fouriera i przedstawia właśnie widmo gęstości amplitudy nieokresowego przebiegu czasowego x(t).
stanowi transformatę Fouriera i przedstawia właśnie widmo gęstości amplitudy nieokresowego przebiegu czasowego x(t).Istotne znaczenie w teorii sygnałów ma również widmo gęstości energii oraz widmo gęstości mocy, opisujące rozkład odpowiednio energii i mocy średniej sygnału w zależności od częstotliwości. W praktyce występuje niekiedy widmo mieszane, tj. połączenie widma dyskretnego i ciągłego, co odpowiada w dziedzinie czasu mieszaninie sygnału okresowego i nieokresowego (zdeterminowanego lub losowego).
Zarówno w zagadnieniach teoretycznych, jak i w praktyce, każdy sygnał, reprezentujący przebieg pewnej wielkości fizycznej, może więc być analizowany albo w dziedzinie czasu — badanie przebiegu funkcji x(t), albo w dziedzinie częstotliwości — badanie przebiegu funkcji X(f). Typowym przyrządem wyznaczającym przebieg funkcji x(t) jest oscyloskop, zaś funkcji X(f) — spektrometr. Obie metody analizy sygnałów są stosowane prawie we wszystkich dziedzinach nauki i techniki, m.in. w biologii, medycynie, astronomii.