szereg Fouriera

szereg Fouriera,

mat. szereg trygonometryczny postaci:

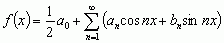(1)

za pomocą którego można przedstawić — przy stosunkowo szerokich założeniach co do funkcji f(x) — funkcję okresową f(x) o okresie 2π (mówi się wtedy o jej rozwinięciu na (lub w) szereg Furiera); wtedy:

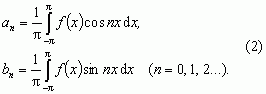
Współczynniki a_n i b_n nazywają się współczynnikami Fouriera funkcji f(x), a wzory (2) — wzorami Eulera–Fouriera. Szereg (1) można również zapisać w postaci:

,

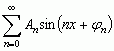gdzie A_nsinφ_n  = a_n oraz A_ncosφ_n = b_n, czyli — przy interpretacji mechanicznej — w postaci nieskończonej sumy drgań harmonicznych (tzw. składowych harmonicznych lub fourierowskich) o amplitudach A_n, różnicach faz φ_n i okresach 2π/n, przy czym zmienna x odgrywa rolę czasu. Wzór (1) można też zapisać w postaci zespolonej:

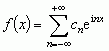, gdzie

.

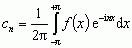Metodę rozwinięcia w szereg Fouriera do rozwiązania konkretnego problemu fiz. pierwszy zastosował (1807) J.B.J. Fourier.