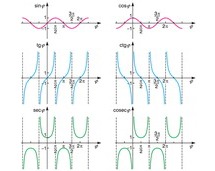
trygonometria dzieli się na płaską i sferyczną; w trygonometrii płaskiej bada się własności trójkątów (wielokątów) położonych na płaszczyźnie, w trygonometrii sferycznej — na powierzchni kuli, przy czym np. w przypadku płaszczyzny można poza geometrią euklidesową rozważać geometrię hiperboliczną (geometria Łobaczewskiego) lub eliptyczną (geometrie Riemanna).
Podstawowe wzory trygonometrii płaskiej (euklidesowej). W przypadku trójkąta o bokach
a,
b,
c, kątach wewnętrznych
α,
β,
γ (
α +
β +
γ = π), obwodzie
a +
b +
c = 2
p i polu
S prawdziwe są następujące wzory: wzór sinusów (
sinusów twierdzenie, sformułowane przez Nasira ad-Din, XIII w.); wzór cosinusów (
cosinusów twierdzenie, w niejawnej postaci występuje już w
Elementach Euklidesa), wzór tangensów (
tangensów twierdzenie, sformułowane przez Regiomontanusa, XV w.) oraz wzory na pole trójkąta:
wzory wiążące kąty trójkąta z jego bokami:
Podstawowe wzory trygonometrii sferycznej. W przypadku trójkąta sferycznego między jego kątami płaskimi
α,
β,
γ i bokami
a,
b,
c (boki
a,
b,
c mierzy się za pomocą odpowiadających im kątów środkowych; długości tych boków są równe odpowiednio
aR,
bR,
cR, gdzie
R — promień sfery) zachodzą następujące wzory:
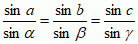
(Abu al-Wafa, X w.),
cos a = cos b · cos c + sin b · sin c · cos α
(Regiomontanus, XV w.),
cos α = –cos β · cos γ + sin β · sin γ · cos a
(F. Viète, 2. połowa XVI w.),
sin a · sin β = cos b · sin c – sin b · cos c · cos α,
sin α · cos b = cos β · sin γ + sin β · cos γ · cos a
(L. Euler, XVIII w.).
Za pomocą przestawień cyklicznych α → β → γ → α oraz a → b → c → a można otrzymać dalsze wzory trygonometrii sferycznej; wzory te pozwalają wyznaczyć 3 dowolne elementy trójkąta sferycznego, gdy znane są pozostałe 3 elementy; trygonometria sferyczna znajduje szerokie zastosowanie w astronomii.
Trygonometrię płaską zapoczątkowali Al-Battani (IX–X w.), Abu al-Wafa, A. Bhaskara, Nasir ad-Din; później rozwijali ją M. Kopernik, Tycho Brahe, J. Kepler; współczesną postać nadał jej Euler. Trygonometria sferyczna powstała znacznie wcześniej (Menelaos z Aleksandrii, Klaudiusz Ptolemeusz) niż trygonometria płaska; wszystkie przypadki rozwiązywania dowolnych trójkątów sferycznych zbadał Nasir ad-Din, a pełny zestaw wzorów trygonometrii sferycznej podał Euler.

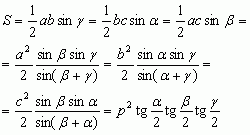
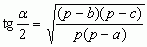
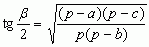
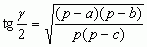
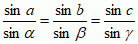 (Abu al-Wafa, X w.),
(Abu al-Wafa, X w.),