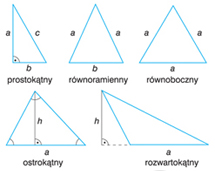
trójkąt,
mat. figura geometryczna płaska będąca zbiorem punktów płaszczyzny ograniczonym łamaną zamkniętą, złożoną z 3 odcinków a, b, c, zwanych bokami trójkąta;
trójkąt
Encyklopedia PWN
punkty A, B, C, leżące na końcach tych odcinków są wierzchołkami trójkąta; pary boków tworzą 3 kąty wewnętrzne trójkąta: α, β, γ; jest wielokątem o najmniejszej liczbie boków; jeden z boków nazywa się podstawą trójkąta, a 2 pozostałe — jego ramionami; odcinek (oraz jego długość), którego końcami są jeden z wierzchołków trójkąta i jego rzut prostokątny na przeciwległy bok (lub jego przedłużenie), jest nazywany wysokością trójkąta; trójkąt jest: równoboczny, równoramienny, różnoboczny, jeżeli ma odpowiednio: wszystkie boki równe, 2 boki równe, wszystkie boki różne; długość dowolnego boku trójkąta jest mniejsza od sumy długości pozostałych boków; trójkąt jest: ostrokątny, prostokątny, rozwartokątny, jeżeli ma odpowiednio: wszystkie kąty wewnętrzne ostre (tzn. mniejsze niż 90°), 1 kąt prosty (równy 90°), 1 kąt rozwarty (większy niż 90°); suma kątów wewnętrznych trójkąta jest równa 180°; na każdym trójkącie można opisać okrąg oraz w każdy trójkąt można wpisać okrąg; środek okręgu opisanego leży w punkcie przecięcia się symetralnych boków trójkąta, a środek okręgu wpisanego — na przecięciu się dwusiecznych kątów trójkąta; środek ciężkości trójkąta leży na przecięciu środkowych trójkąta; punkt przecięcia wysokości trójkąta nazywa się ortocentrum trójkąta; badaniem związków między bokami a kątami trójkąta zajmuje się trygonometria; pole trójkąta wyraża się wzorami: ah/2, bcsinα/2, abc/(4R), rp, 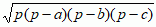 (wzór Herona), gdzie a, b, c — długości boków trójkąta, h — wysokość opuszczona na bok a, α — kąt między bokami b i c, R — promień okręgu opisanego na trójkącie, r — promień okręgu wpisanego, p — połowa obwodu trójkąta, tzn. p = (a + b + c)/2.
(wzór Herona), gdzie a, b, c — długości boków trójkąta, h — wysokość opuszczona na bok a, α — kąt między bokami b i c, R — promień okręgu opisanego na trójkącie, r — promień okręgu wpisanego, p — połowa obwodu trójkąta, tzn. p = (a + b + c)/2.
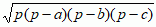 (wzór Herona), gdzie a, b, c — długości boków trójkąta, h — wysokość opuszczona na bok a, α — kąt między bokami b i c, R — promień okręgu opisanego na trójkącie, r — promień okręgu wpisanego, p — połowa obwodu trójkąta, tzn. p = (a + b + c)/2.
(wzór Herona), gdzie a, b, c — długości boków trójkąta, h — wysokość opuszczona na bok a, α — kąt między bokami b i c, R — promień okręgu opisanego na trójkącie, r — promień okręgu wpisanego, p — połowa obwodu trójkąta, tzn. p = (a + b + c)/2.