liczby zespolone,
mat. liczby postaci z = a + bi, gdzie a oraz b są liczbami rzeczywistymi, nazywanymi odpowiednio częścią rzeczywistą oraz częścią urojoną z, oznaczanymi a = Re z, b = Im z, a i — jednostką urojoną, tzn. liczbą, która ma własność i2 = –1;
liczby zespolone
Encyklopedia PWN
liczbę x nazywa się częścią rzeczywistą liczby z i oznacza symbolem Re z, liczbę y nazywa się częścią urojoną liczby z i oznacza symbolem Im z; liczby zespolone postaci z = a + 0i utożsamia się z liczbą rzeczywistą a — liczby rzeczywiste są więc podzbiorem zbioru liczb zespolonych; działania na liczbach zespolonych wykonuje się tak jak na wyrażeniach algebraicznych, np. dodawanie i odejmowanie: (a + ib)± (c + id) = (a ± c) + (b ± d)i, mnożenie: (a + ib) · (c + id) = (ac –bd) + i(ad + bc), dzielenie:
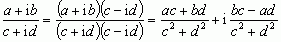
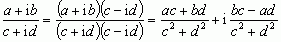
dodawanie i mnożenie są działaniami łącznymi, mnożenie jest rozdzielne względem dodawania, a dzielenie przez liczbę z ≠ 0 (tzn. z ≠ 0 + i0) jest zawsze wykonalne.
Liczby zespolone wprowadza się właściwie jako zbiór uporządkowanych par liczb rzeczywistych (a, b) i na elementach tego zbioru określa się działania dodawania i odejmowania: (a, b) ⊕ (c, d) = (a + c, b + d), (a, b) ⊖ (c, d) = (a – c, b – d), mnożenia: (a, b) ⊙ (c, d) = (ac – bd, ad + bc) i dzielenia:
(a, b) 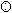 (c, d) =
(c, d) = 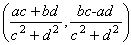 ;
;
 (c, d) =
(c, d) = 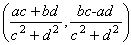 ;
; pary postaci (a, 0) utożsamia się z liczbami rzeczywistymi i przyjmuje prostszy zapis: (a, 0) ≡ a, zaś pary postaci (0, b) utożsamia się z liczbami urojonymi i przyjmuje zapis (0, b) = (b, 0) ⊙ (0, 1) = bi, gdzie para (0, 1) oznaczona jest literą i (jednostka urojona); stąd też (a, b) = a + bi. Liczby zespolone z = a + bi interpretuje się jako punkt płaszczyzny o współrzędnych (a, b) lub jako wektor wodzący o tychże współrzędnych (a, b) — płaszczyzna ta nosi nazwę płaszczyzny zespolonej lub płaszczyzny Gaussa.
Liczby zespolone z = x + iy oraz 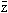 = x –iy nazywa się liczbami zespolonymi sprzężonymi, odległość |z| punktu z od początku układu współrzędnych 0 — modułem albo wartością bezwzględną liczby zespolonej z,
= x –iy nazywa się liczbami zespolonymi sprzężonymi, odległość |z| punktu z od początku układu współrzędnych 0 — modułem albo wartością bezwzględną liczby zespolonej z, 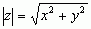 . Liczbę zespoloną można przedstawić w tzw. postaci trygonometrycznej z = |z| · (cos φ + i sin φ); kąt φ nosi nazwę argumentu liczby zespolonej z ≠ 0; liczba zespolona z ≠ 0 ma nieskończenie wiele argumentów: arg z = φ + 2kπ (k — dowolna liczba całkowita); ta wartość kąta φ, która spełnia warunek –π < φ ≤ +π, jest zwana argumentem głównym liczby zespolonej z. Liczbę zespoloną z można również zapisać w postaci wykładniczej: z = | z| eiφ (korzystając ze wzoru Eulera, że eiφ = cos φ + i sin φ); z tej ostatniej postaci wynika, że przy mnożeniu 2 liczb zespolonych
. Liczbę zespoloną można przedstawić w tzw. postaci trygonometrycznej z = |z| · (cos φ + i sin φ); kąt φ nosi nazwę argumentu liczby zespolonej z ≠ 0; liczba zespolona z ≠ 0 ma nieskończenie wiele argumentów: arg z = φ + 2kπ (k — dowolna liczba całkowita); ta wartość kąta φ, która spełnia warunek –π < φ ≤ +π, jest zwana argumentem głównym liczby zespolonej z. Liczbę zespoloną z można również zapisać w postaci wykładniczej: z = | z| eiφ (korzystając ze wzoru Eulera, że eiφ = cos φ + i sin φ); z tej ostatniej postaci wynika, że przy mnożeniu 2 liczb zespolonych 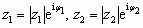 moduły ich mnoży się, a argumenty dodaje:
moduły ich mnoży się, a argumenty dodaje: 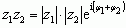 ; w szczególności wynika stąd wzór de Moivre’a: zn = [|z|(cos φ + i sin φ)]n = |z|n(cos nφ + i sin nφ) oraz wzór na wszystkie n różnych pierwiastków stopnia n z liczby zespolonej z:
; w szczególności wynika stąd wzór de Moivre’a: zn = [|z|(cos φ + i sin φ)]n = |z|n(cos nφ + i sin nφ) oraz wzór na wszystkie n różnych pierwiastków stopnia n z liczby zespolonej z: 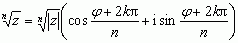 , gdzie k = 0, 1, 2,... , n –1. Liczby zespolone znalazły wiele zastosowań w matematyce, fizyce, technice.
, gdzie k = 0, 1, 2,... , n –1. Liczby zespolone znalazły wiele zastosowań w matematyce, fizyce, technice.
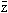 = x –iy nazywa się liczbami zespolonymi sprzężonymi, odległość |z| punktu z od początku układu współrzędnych 0 — modułem albo wartością bezwzględną liczby zespolonej z,
= x –iy nazywa się liczbami zespolonymi sprzężonymi, odległość |z| punktu z od początku układu współrzędnych 0 — modułem albo wartością bezwzględną liczby zespolonej z, 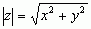 . Liczbę zespoloną można przedstawić w tzw. postaci trygonometrycznej z = |z| · (cos φ + i sin φ); kąt φ nosi nazwę argumentu liczby zespolonej z ≠ 0; liczba zespolona z ≠ 0 ma nieskończenie wiele argumentów: arg z = φ + 2kπ (k — dowolna liczba całkowita); ta wartość kąta φ, która spełnia warunek –π < φ ≤ +π, jest zwana argumentem głównym liczby zespolonej z. Liczbę zespoloną z można również zapisać w postaci wykładniczej: z = | z| eiφ (korzystając ze wzoru Eulera, że eiφ = cos φ + i sin φ); z tej ostatniej postaci wynika, że przy mnożeniu 2 liczb zespolonych
. Liczbę zespoloną można przedstawić w tzw. postaci trygonometrycznej z = |z| · (cos φ + i sin φ); kąt φ nosi nazwę argumentu liczby zespolonej z ≠ 0; liczba zespolona z ≠ 0 ma nieskończenie wiele argumentów: arg z = φ + 2kπ (k — dowolna liczba całkowita); ta wartość kąta φ, która spełnia warunek –π < φ ≤ +π, jest zwana argumentem głównym liczby zespolonej z. Liczbę zespoloną z można również zapisać w postaci wykładniczej: z = | z| eiφ (korzystając ze wzoru Eulera, że eiφ = cos φ + i sin φ); z tej ostatniej postaci wynika, że przy mnożeniu 2 liczb zespolonych 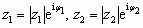 moduły ich mnoży się, a argumenty dodaje:
moduły ich mnoży się, a argumenty dodaje: 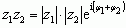 ; w szczególności wynika stąd wzór de Moivre’a: zn = [|z|(cos φ + i sin φ)]n = |z|n(cos nφ + i sin nφ) oraz wzór na wszystkie n różnych pierwiastków stopnia n z liczby zespolonej z:
; w szczególności wynika stąd wzór de Moivre’a: zn = [|z|(cos φ + i sin φ)]n = |z|n(cos nφ + i sin nφ) oraz wzór na wszystkie n różnych pierwiastków stopnia n z liczby zespolonej z: 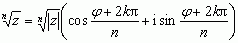 , gdzie k = 0, 1, 2,... , n –1. Liczby zespolone znalazły wiele zastosowań w matematyce, fizyce, technice.
, gdzie k = 0, 1, 2,... , n –1. Liczby zespolone znalazły wiele zastosowań w matematyce, fizyce, technice. 

