jednostka urojona
Encyklopedia PWN
mat. liczby zespolone postaci bi, gdzie b — liczba rzeczywista, i — jednostka urojona;
mat. liczby postaci z = a + bi, gdzie a oraz b są liczbami rzeczywistymi, nazywanymi odpowiednio częścią rzeczywistą oraz częścią urojoną z, oznaczanymi a = Re z, b = Im z, a i — jednostką urojoną, tzn. liczbą, która ma własność i2 = 
;
;
austr. psychiatra i psycholog, twórca kierunku zw. psychologią indywidualną.
epimorfizm
mat. homomorfizm g danej algebry uniwersalnej A (grupy, pierścienia, ciała, przestrzeni liniowej, algebry Boole’a itp.) „na” daną algebrę uniwersalną B, tzn. taki, że każdy element B jest obrazem jakiegoś elementu z A;
[gr.],
Fouriera przekształcenie, transformacja Fouriera,
mat. przyporządkowanie (transformacja), w którym danej funkcji f(x) odpowiada funkcja F(λ) =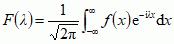 
(1) (czynnik 1/
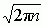jest przez niektórych autorów włączany do f(x), i — jednostka urojona);
