liczby rzeczywiste,
mat. wspólna nazwa dla liczb wymiernych i niewymiernych;
liczby rzeczywiste
Encyklopedia PWN
zbiór liczb rzeczywistych oznacza się literą ℝ. Każda liczba rzeczywista ma rozwinięcie na ułamek dziesiętny nieskończony, np. 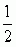 = 0,5000... ,
= 0,5000... , 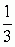 = 0,333... , π = 3,14159...; gdy rozwinięcie to jest od pewnego miejsca okresowe, tzn. gdy od pewnego miejsca pewna grupa cyfr powtarza się, np. 37,5828282... , to dana liczba rzeczywista jest liczbą wymierną. Liczby rzeczywiste można utożsamiać z punktami prostej (tzw. prosta lub oś liczbowa). Liczby rzeczywiste spełniają następujące aksjomaty (a, b, c, x — dowolne liczby rzeczywiste): 1) a + b = b + a (przemienność dodawania); 2) (a + b) + c = a + (b + c) (łączność dodawania); 3) istnieje jedyna liczba x spełniająca równanie a + x = b; liczbę tę oznacza się b − a; 4) ab = ba (przemienność mnożenia); 5) (ab)c = a(bc) (łączność mnożenia); 6) istnieje jedyna liczba x spełniająca równanie ax = b (dla a ≠ 0); liczbę tę oznacza się b/a; 7) a(b + c) = ab + ac (rozdzielność mnożenia względem dodawania); 8) albo a < 0, albo a = 0, albo a > 0; 9) jeżeli a > 0 i b > 0, to a + b > 0 i ab > 0; 10) dowolny zbiór liczb rzeczywistych ograniczony z góry ma kres górny (kres zbioru). Najbardziej znane definicje (konstrukcje) liczb rzeczywistych to: definicja Dedekinda (Dedekinda przekrój), definicja Cantora — oparta na pojęciu ciągów liczb wymiernych spełniających warunek Cauchy’ego, definicja Weierstrassa — oparta na teorii ułamków dziesiętnych nieskończonych.
= 0,333... , π = 3,14159...; gdy rozwinięcie to jest od pewnego miejsca okresowe, tzn. gdy od pewnego miejsca pewna grupa cyfr powtarza się, np. 37,5828282... , to dana liczba rzeczywista jest liczbą wymierną. Liczby rzeczywiste można utożsamiać z punktami prostej (tzw. prosta lub oś liczbowa). Liczby rzeczywiste spełniają następujące aksjomaty (a, b, c, x — dowolne liczby rzeczywiste): 1) a + b = b + a (przemienność dodawania); 2) (a + b) + c = a + (b + c) (łączność dodawania); 3) istnieje jedyna liczba x spełniająca równanie a + x = b; liczbę tę oznacza się b − a; 4) ab = ba (przemienność mnożenia); 5) (ab)c = a(bc) (łączność mnożenia); 6) istnieje jedyna liczba x spełniająca równanie ax = b (dla a ≠ 0); liczbę tę oznacza się b/a; 7) a(b + c) = ab + ac (rozdzielność mnożenia względem dodawania); 8) albo a < 0, albo a = 0, albo a > 0; 9) jeżeli a > 0 i b > 0, to a + b > 0 i ab > 0; 10) dowolny zbiór liczb rzeczywistych ograniczony z góry ma kres górny (kres zbioru). Najbardziej znane definicje (konstrukcje) liczb rzeczywistych to: definicja Dedekinda (Dedekinda przekrój), definicja Cantora — oparta na pojęciu ciągów liczb wymiernych spełniających warunek Cauchy’ego, definicja Weierstrassa — oparta na teorii ułamków dziesiętnych nieskończonych.
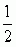 = 0,5000... ,
= 0,5000... , 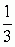 = 0,333... , π = 3,14159...; gdy rozwinięcie to jest od pewnego miejsca okresowe, tzn. gdy od pewnego miejsca pewna grupa cyfr powtarza się, np. 37,5828282... , to dana liczba rzeczywista jest liczbą wymierną. Liczby rzeczywiste można utożsamiać z punktami prostej (tzw. prosta lub oś liczbowa). Liczby rzeczywiste spełniają następujące aksjomaty (a, b, c, x — dowolne liczby rzeczywiste): 1) a + b = b + a (przemienność dodawania); 2) (a + b) + c = a + (b + c) (łączność dodawania); 3) istnieje jedyna liczba x spełniająca równanie a + x = b; liczbę tę oznacza się b − a; 4) ab = ba (przemienność mnożenia); 5) (ab)c = a(bc) (łączność mnożenia); 6) istnieje jedyna liczba x spełniająca równanie ax = b (dla a ≠ 0); liczbę tę oznacza się b/a; 7) a(b + c) = ab + ac (rozdzielność mnożenia względem dodawania); 8) albo a < 0, albo a = 0, albo a > 0; 9) jeżeli a > 0 i b > 0, to a + b > 0 i ab > 0; 10) dowolny zbiór liczb rzeczywistych ograniczony z góry ma kres górny (kres zbioru). Najbardziej znane definicje (konstrukcje) liczb rzeczywistych to: definicja Dedekinda (Dedekinda przekrój), definicja Cantora — oparta na pojęciu ciągów liczb wymiernych spełniających warunek Cauchy’ego, definicja Weierstrassa — oparta na teorii ułamków dziesiętnych nieskończonych.
= 0,333... , π = 3,14159...; gdy rozwinięcie to jest od pewnego miejsca okresowe, tzn. gdy od pewnego miejsca pewna grupa cyfr powtarza się, np. 37,5828282... , to dana liczba rzeczywista jest liczbą wymierną. Liczby rzeczywiste można utożsamiać z punktami prostej (tzw. prosta lub oś liczbowa). Liczby rzeczywiste spełniają następujące aksjomaty (a, b, c, x — dowolne liczby rzeczywiste): 1) a + b = b + a (przemienność dodawania); 2) (a + b) + c = a + (b + c) (łączność dodawania); 3) istnieje jedyna liczba x spełniająca równanie a + x = b; liczbę tę oznacza się b − a; 4) ab = ba (przemienność mnożenia); 5) (ab)c = a(bc) (łączność mnożenia); 6) istnieje jedyna liczba x spełniająca równanie ax = b (dla a ≠ 0); liczbę tę oznacza się b/a; 7) a(b + c) = ab + ac (rozdzielność mnożenia względem dodawania); 8) albo a < 0, albo a = 0, albo a > 0; 9) jeżeli a > 0 i b > 0, to a + b > 0 i ab > 0; 10) dowolny zbiór liczb rzeczywistych ograniczony z góry ma kres górny (kres zbioru). Najbardziej znane definicje (konstrukcje) liczb rzeczywistych to: definicja Dedekinda (Dedekinda przekrój), definicja Cantora — oparta na pojęciu ciągów liczb wymiernych spełniających warunek Cauchy’ego, definicja Weierstrassa — oparta na teorii ułamków dziesiętnych nieskończonych. 

