logarytm
mat. logarytm liczby b przy podstawie a, oznaczany logab, to liczba, do której należy podnieść liczbę a, by uzyskać liczbę b;
[gr. lógos ‘słowo’, arithmós ‘liczba’],
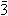 ,3010... , log 0,0503 = 2,&siedemmacr.x;016... itp.; przybliżone wartości mantys logarytmów liczb są zapisane w tablicach logarytmicznych.
,3010... , log 0,0503 = 2,&siedemmacr.x;016... itp.; przybliżone wartości mantys logarytmów liczb są zapisane w tablicach logarytmicznych. 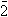 + 0,6990.
+ 0,6990. 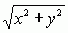 + i(φ + 2kπ), gdzie φ = arctg(y/x) oznacza argument główny logarytmowanej liczby zespolonej (−π < φ < +π), a liczba k = 0, ±1, ±2, ...; dla k = 0 otrzymuje się liczbę zwaną wartością główną logarytmu liczby zespolonej z.
+ i(φ + 2kπ), gdzie φ = arctg(y/x) oznacza argument główny logarytmowanej liczby zespolonej (−π < φ < +π), a liczba k = 0, ±1, ±2, ...; dla k = 0 otrzymuje się liczbę zwaną wartością główną logarytmu liczby zespolonej z.