kwaterniony
Encyklopedia PWN
każdy kwaternion ma postać q = a + bi + cj + dk, gdzie współrz. a, b, c, d są liczbami rzeczywistymi, a jednostki podstawowe i, j, k spełniają warunki: i2 = j2 = k2 = ijk = −1; można zatem uważać kwaterniony za wektory przestrzeni czterowymiarowej; powyższe równości pozwalają zdefiniować mnożenie kwaternionów (jest ono nieprzemienne), np. i · j = −j · i = k, j · k = −k · j = i, k · i = −i · k = j; kwaterniony zatem tworzą pierścień, w którym każdy niezerowy element posiada element odwrotny; kwaterniony można również uważać za macierze zespolone postaci 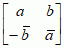 , gdzie
, gdzie 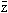 oznacza liczbę sprzężoną do z. Zostały odkryte 1843 przez W.R. Hamiltona; znalazły zastosowanie w geometrii przestrzeni trójwymiarowej, mechanice klas., mechanice kwantowej i w termodynamice.
oznacza liczbę sprzężoną do z. Zostały odkryte 1843 przez W.R. Hamiltona; znalazły zastosowanie w geometrii przestrzeni trójwymiarowej, mechanice klas., mechanice kwantowej i w termodynamice.
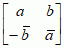 , gdzie
, gdzie 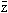 oznacza liczbę sprzężoną do z. Zostały odkryte 1843 przez W.R. Hamiltona; znalazły zastosowanie w geometrii przestrzeni trójwymiarowej, mechanice klas., mechanice kwantowej i w termodynamice.
oznacza liczbę sprzężoną do z. Zostały odkryte 1843 przez W.R. Hamiltona; znalazły zastosowanie w geometrii przestrzeni trójwymiarowej, mechanice klas., mechanice kwantowej i w termodynamice. 

