pierścień,
mat. niepusty zbiór R, w którym określono 2 działania, przyporządkowujące każdej parze (a, b) elementów z R jeden element z R: dodawanie (a, b)  a+b i mnożenie (a, b)
a+b i mnożenie (a, b)  ab; działania te muszą spełniać następujące aksjomaty: 1) R jest grupą przemienną względem dodawania; 2) dla każdego a, b, c ∈ R zachodzi (a + b)c = ac + bc (prawostronna rozdzielność mnożenia względem dodawania); 3) dla każdego a, b, c ∈ R zachodzi a(b + c) = ab + ac (lewostronna rozdzielność mnożenia względem dodawania).
ab; działania te muszą spełniać następujące aksjomaty: 1) R jest grupą przemienną względem dodawania; 2) dla każdego a, b, c ∈ R zachodzi (a + b)c = ac + bc (prawostronna rozdzielność mnożenia względem dodawania); 3) dla każdego a, b, c ∈ R zachodzi a(b + c) = ab + ac (lewostronna rozdzielność mnożenia względem dodawania).

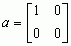 ,
, 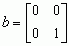 to
to 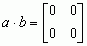 — a więc a i b są dzielnikami zera w pierścieniu macierzy stopnia 2; taki element j pierścienia, że j · x = x · j = x dla każdego elementu x, nazywa się
— a więc a i b są dzielnikami zera w pierścieniu macierzy stopnia 2; taki element j pierścienia, że j · x = x · j = x dla każdego elementu x, nazywa się 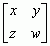 o zespolonych elementach; 5) zbiór funkcji ciągłych f, g, h, ... o wartościach zespolonych, określonych w przedziale [0; +∞) z działaniami (+) i (·) określonymi następująco: f = g + h, jeśli f (x) = g(x) + h(x) dla każdego x ≥ 0, f = g · h, jeśli
o zespolonych elementach; 5) zbiór funkcji ciągłych f, g, h, ... o wartościach zespolonych, określonych w przedziale [0; +∞) z działaniami (+) i (·) określonymi następująco: f = g + h, jeśli f (x) = g(x) + h(x) dla każdego x ≥ 0, f = g · h, jeśli 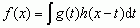 ; pierścień ten nazywa się pierścieniem Mikusińskiego — nie ma on ani elementu jednostkowego, ani też dzielników zera.
; pierścień ten nazywa się pierścieniem Mikusińskiego — nie ma on ani elementu jednostkowego, ani też dzielników zera.
