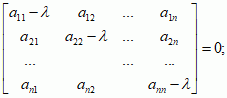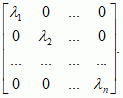Dowolna macierz A o m wierszach i n kolumnach (macierz m × n), o składowych aij, ma postać
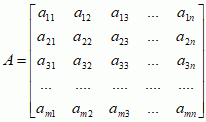
; np. macierz
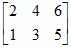
ma 2 wiersze i 3 kolumny. Jeżeli liczba wierszy
m jest równa liczbie kolumn
n, to macierz nazywa się
kwadratową,
n — jej
stopniem, a sumę jej elementów
a11 +
a22 + ... +
ann —
śladem. Symbolem det
A oznacza się
wyznacznik macierzy kwadratowej
A; jeżeli det
A = 0, to
A nazywa się
macierzą osobliwą, a w przypadku przeciwnym —
nieosobliwą (det
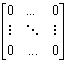
A ≠ 0). Macierz postaci:
Jeżeli A = [aij] oraz B = [bij] są macierzami m × n, to można je dodać: składowymi macierzy C = A + B są elementy cij = aij + bij dla dowolnych i, j. Jeżeli A = [aij] jest macierzą m × n, a B = [bij] macierzą n × k, to ich iloczyn D = A·B jest macierzą m × k o składowych dij, określonych wzorem dij = ai1b1j + ai2b2j + ... + ainbnj dla i = 1, ... , m, j = 1, ... , k. Zatem, aby pomnożyć dwie macierze, mnoży się kolejne wiersze pierwszej z nich przez kolumny drugiej, np.
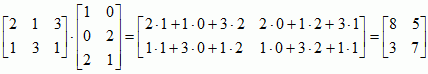
.
Dodawanie macierzy podlega prawom łączności i przemienności, mnożenie zaś podlega prawom łączności i rozdzielności mnożenia względem dodawania; mnożenie macierzy na ogół nie jest przemienne, tzn. na ogół A · B ≠ B · A, np.
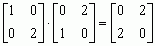
, a
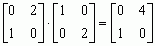
.
Elementem neutralnym mnożenia macierzy kwadratowych jest macierz jednostkowa (A · I = I · A = A). Zbiór macierzy kwadratowych Mn(R) o składowych z pierścienia R jest również pierścieniem (z działaniami dodawania i mnożenia macierzy).
Jeżeli w macierzy prostokątnej
A skreśli się pewną liczbę wierszy oraz pewną liczbę kolumn, tak by pozostałe elementy tworzyły macierz kwadratową
M (podmacierz), to jej wyznacznik det
M nazywa się
minorem macierzy A; przykładami minorów macierzy
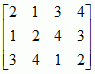
są:
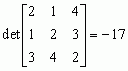
,
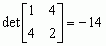
, det[2] = 2; są to minory, odpowiednio, trzeciego, drugiego i pierwszego stopnia. Najwyższy ze stopni niezerowych minorów nazywa się
rzędem macierzy. Jeśli w macierzy
A = [
aik] zamieni się kolumny na wiersze i na odwrót, to otrzymana macierz
AT = [
aki] nazywa się
macierzą przestawioną lub
transponowaną. Dla macierzy kwadratowej
A = [
aik] macierz o elementach
bik = (–1)
i + kMki/det
A, gdzie
Mki oznacza minor otrzymany po skreśleniu w macierzy
A k-tego wiersza i
i-tej kolumny, nazywa się
macierzą odwrotną do
A i oznacza symbolem
A–1 (
AA–1 =
A–1A =
I). Jeżeli elementy
aik macierzy
A są liczbami zespolonymi, to macierz
Ā o elementach
āik, sprzężonych względem elementów
aik, nazywa się
macierzą sprzężoną względem macierzy
A; macierz jest symetryczna — gdy
AT =
A, ortogonalna — gdy
AT =
A–1, hermitowska — gdy
AT =
Ā, unitarna — gdy
ĀT =
A–1. Dwie macierze kwadratowe
A i
B tego samego stopnia nazywają się
równoważnymi (lub
podobnymi) wtedy i tylko wtedy, gdy istnieje macierz kwadratowa nieosobliwa
T, taka że
A =
T–1BT.
Ważnym (ze względu na zastosowania) problemem teorii macierzy jest zagadnienie sprowadzania danej macierzy kwadratowej
A do postaci kanonicznej, np. do postaci diagonalnej. W tym celu rozwiązuje się
równanie charakterystyczne:
Jeżeli to równanie ma
n różnych pierwiastków
λ1,
λ2, ... ,
λn, to dana macierz
A jest równoważna macierzy:
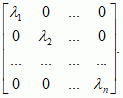
Elementy aik macierzy A można interpretować jako współczynniki przekształcenia liniowego:
y1 = a11 x1 + a12x2 + ... + a1nxn
....................................................
ym = am1x1 + am2x2 + ... + amnxn.
Wówczas macierz A = [aik] nazywa się macierzą tego przekształcenia. Zatem można to przekształcenie zapisać krótko w postaci macierzowej: y = AxT, gdzie x i y oznaczają macierze jednokolumnowe [x1, ... , xn] i [y1, ... , ym].
Macierze są wszechstronnie stosowanym narzędziem matematyki: opisują układy równań liniowych, algebraicznych i różniczkowych, przekształcenia liniowe, stożkowe i kwadryki, mają zastosowania w analizie matematycznej i geometrii różniczkowej, odgrywają zasadniczą rolę w algebrze nieprzemiennej itd. Powstanie pojęcia macierzy, jak też początki rachunku macierzowego przypadają na połowę XIX w. (prace A. Cayleya i E. Laguerre’a). Podstawy teorii macierzy jako dyscypliny algebraicznej stworzyli K. Weierstrass, C. Jordan i F.G. Frobenius w 2. połowie XIX w.

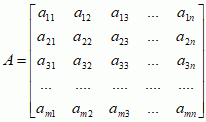 ; np. macierz
; np. macierz 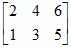 ma 2 wiersze i 3 kolumny. Jeżeli liczba wierszy m jest równa liczbie kolumn n, to macierz nazywa się
ma 2 wiersze i 3 kolumny. Jeżeli liczba wierszy m jest równa liczbie kolumn n, to macierz nazywa się  ,
,  ,
, 
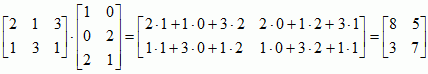 .
. 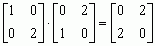 , a
, a 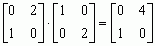 .
. 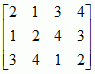 są:
są: 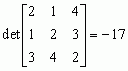 ,
, 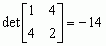 , det[2] = 2; są to minory, odpowiednio, trzeciego, drugiego i pierwszego stopnia. Najwyższy ze stopni niezerowych minorów nazywa się
, det[2] = 2; są to minory, odpowiednio, trzeciego, drugiego i pierwszego stopnia. Najwyższy ze stopni niezerowych minorów nazywa się