przekształcenie liniowe,
mat. jedno z podstawowych pojęć algebry liniowej; funkcję f z przestrzeni liniowej V w przestrzeń liniową W, f: V → W, gdzie V i W są przestrzeniami liniowymi nad tym samym ciałem K, nazywa się p.l., jeżeli zachodzi równość f(λx + μy) = λf(x) + μf(y) dla dowolnych λ, μ ∈ K i x, y ∈ V.
przekształcenie liniowe
Encyklopedia PWN
Jeżeli f jest funkcją różnowartościową i odwzorowuje V „na” W, to f jest izomorfizmem przestrzeni liniowych, np. każda n-wymiarowa przestrzeń liniowa nad ciałem K jest izomorficzna z przestrzenią Kn, złożoną ze wszystkich ciągów (x1, ... , xn) o elementach x1, ... , xn z ciała K. Jeżeli W = K, to p.l. f jest nazywane funkcjonałem liniowym. Przykładowo, p.l. jest funkcja f: ℝ2 → ℝ2 określona dla v = (x, y) wzorem f(v) = (x, 0) (rzut wektora v na oś OX), a funkcjonałem liniowym w przestrzeni funkcji ciągłych C(0, 1) jest funkcja g: C(0, 1) → ℝ określona jako pole pod krzywą y = g(x) w przedziale [0, 1], tzn. funkcja zdefiniowana wzorem: 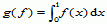 . Zbiór V* wszystkich funkcjonałów liniowych określonych w przestrzeni liniowej V jest również przestrzenią liniową nad K — względem dodawania funkcjonałów (f + g)(v) = f(v) + g(v) i mnożenia przez skalary (λf)(v) = λf(v) (f, g ∈ V*, v ∈ V, λ ∈ K). Jeżeli V i W są przestrzeniami liniowymi skończonego wymiaru (dimKV = n, dimKW = m), e1, ... , en jest bazą V, a f1, ... , fm bazą W, to można mówić o macierzy przekształcenia liniowego f: V → W w bazach e1, ... , en i f1, ... , fm: jest nią macierz A współczynników aij wyrażających obrazy wektorów bazy V jako kombinacje liniowe wektorów bazy W, tzn. jeżeli f(ei) = a1if1 + ... + amifm dla i = 1, ... , n, to tablica współczynników A =
. Zbiór V* wszystkich funkcjonałów liniowych określonych w przestrzeni liniowej V jest również przestrzenią liniową nad K — względem dodawania funkcjonałów (f + g)(v) = f(v) + g(v) i mnożenia przez skalary (λf)(v) = λf(v) (f, g ∈ V*, v ∈ V, λ ∈ K). Jeżeli V i W są przestrzeniami liniowymi skończonego wymiaru (dimKV = n, dimKW = m), e1, ... , en jest bazą V, a f1, ... , fm bazą W, to można mówić o macierzy przekształcenia liniowego f: V → W w bazach e1, ... , en i f1, ... , fm: jest nią macierz A współczynników aij wyrażających obrazy wektorów bazy V jako kombinacje liniowe wektorów bazy W, tzn. jeżeli f(ei) = a1if1 + ... + amifm dla i = 1, ... , n, to tablica współczynników A = 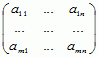 jest macierzą p.l. f; np. macierzą p.l. f, określonego dla v = (x, y) wzorem f(v) = (x, 0), w bazie e1 = (1, 0), e2 = (0, 1) jest macierz A =
jest macierzą p.l. f; np. macierzą p.l. f, określonego dla v = (x, y) wzorem f(v) = (x, 0), w bazie e1 = (1, 0), e2 = (0, 1) jest macierz A = 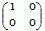 , ponieważ f(e1) = e1 = 1 · e1 + 0 · e2, f(e2) = 0 = 0 · e1 + 0 · e2. Złożenie dwóch p.l. jest p.l.; jeżeli rozpatrywane przestrzenie liniowe są skończonego wymiaru, to macierz superpozycji dwóch p.l. jest iloczynem macierzy tych p.l.
, ponieważ f(e1) = e1 = 1 · e1 + 0 · e2, f(e2) = 0 = 0 · e1 + 0 · e2. Złożenie dwóch p.l. jest p.l.; jeżeli rozpatrywane przestrzenie liniowe są skończonego wymiaru, to macierz superpozycji dwóch p.l. jest iloczynem macierzy tych p.l.
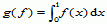 . Zbiór V* wszystkich funkcjonałów liniowych określonych w przestrzeni liniowej V jest również przestrzenią liniową nad K — względem dodawania funkcjonałów (f + g)(v) = f(v) + g(v) i mnożenia przez skalary (λf)(v) = λf(v) (f, g ∈ V*, v ∈ V, λ ∈ K). Jeżeli V i W są przestrzeniami liniowymi skończonego wymiaru (dimKV = n, dimKW = m), e1, ... , en jest bazą V, a f1, ... , fm bazą W, to można mówić o macierzy przekształcenia liniowego f: V → W w bazach e1, ... , en i f1, ... , fm: jest nią macierz A współczynników aij wyrażających obrazy wektorów bazy V jako kombinacje liniowe wektorów bazy W, tzn. jeżeli f(ei) = a1if1 + ... + amifm dla i = 1, ... , n, to tablica współczynników A =
. Zbiór V* wszystkich funkcjonałów liniowych określonych w przestrzeni liniowej V jest również przestrzenią liniową nad K — względem dodawania funkcjonałów (f + g)(v) = f(v) + g(v) i mnożenia przez skalary (λf)(v) = λf(v) (f, g ∈ V*, v ∈ V, λ ∈ K). Jeżeli V i W są przestrzeniami liniowymi skończonego wymiaru (dimKV = n, dimKW = m), e1, ... , en jest bazą V, a f1, ... , fm bazą W, to można mówić o macierzy przekształcenia liniowego f: V → W w bazach e1, ... , en i f1, ... , fm: jest nią macierz A współczynników aij wyrażających obrazy wektorów bazy V jako kombinacje liniowe wektorów bazy W, tzn. jeżeli f(ei) = a1if1 + ... + amifm dla i = 1, ... , n, to tablica współczynników A = 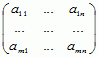 jest macierzą p.l. f; np. macierzą p.l. f, określonego dla v = (x, y) wzorem f(v) = (x, 0), w bazie e1 = (1, 0), e2 = (0, 1) jest macierz A =
jest macierzą p.l. f; np. macierzą p.l. f, określonego dla v = (x, y) wzorem f(v) = (x, 0), w bazie e1 = (1, 0), e2 = (0, 1) jest macierz A = 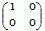 , ponieważ f(e1) = e1 = 1 · e1 + 0 · e2, f(e2) = 0 = 0 · e1 + 0 · e2. Złożenie dwóch p.l. jest p.l.; jeżeli rozpatrywane przestrzenie liniowe są skończonego wymiaru, to macierz superpozycji dwóch p.l. jest iloczynem macierzy tych p.l.
, ponieważ f(e1) = e1 = 1 · e1 + 0 · e2, f(e2) = 0 = 0 · e1 + 0 · e2. Złożenie dwóch p.l. jest p.l.; jeżeli rozpatrywane przestrzenie liniowe są skończonego wymiaru, to macierz superpozycji dwóch p.l. jest iloczynem macierzy tych p.l. Witold Więsław


