macierzy przekształcenia liniowego
Encyklopedia PWN
mat. jedno z podstawowych pojęć algebry liniowej; funkcję f z przestrzeni liniowej V w przestrzeń liniową W, f: V → W, gdzie V i W są przestrzeniami liniowymi nad tym samym ciałem K, nazywa się p.l., jeżeli zachodzi równość f(λx + μy) = λf(x) + μf(y) dla dowolnych λ, μ ∈ K i x, y ∈ V.
mat. dwuwskaźnikowa tablica, której elementy pochodzą z ustalonego pierścienia R (można utworzyć macierz z liczb, funkcji itp.).
mat. macierz (aij)1≤i,j≤n o wyrazach zespolonych, spełniająca warunek: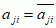 
dla wszystkich i, j (macierz);
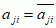dla wszystkich i, j (macierz);
dział algebry poświęcony badaniu przestrzeni liniowych, przekształceń liniowych, form: liniowych, dwuliniowych, wieloliniowych, kwadratowych, określonych na przestrzeniach liniowych, a w szczególności — badaniu macierzy, wyznaczników i równań liniowych;
mat. dział matematyki poświęcony opisowi grup (grupa) — struktur algebraicznych najczęściej spotykanych w matematyce i jej zastosowaniach.
