różniczka funkcji,
mat. pochodna funkcji wielu zmiennych rzeczywistych; mówi się, że funkcja f = (f1, ... , fn): ℝm → ℝn ma różniczkę zupełną Df(x) = A w punkcie x, jeśli istnieje przekształcenie liniowe A: ℝm → ℝn, takie że 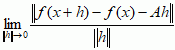 = 0;
= 0;
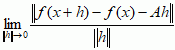 = 0;
= 0;
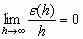 ; wyrażenie dy = f′(x0) · h, będące funkcją liniową przyrostu h, nazywa się różniczkę funkcji y = f(x) obliczoną w punkcie x0 dla przyrostu h (który często oznacza się przez dx i nazywa różniczką argumentu funkcji y = f(x)); analogicznie dla funkcji 2 zmiennych z = f(x, y) różniczkę dz definiuje się wzorem:
; wyrażenie dy = f′(x0) · h, będące funkcją liniową przyrostu h, nazywa się różniczkę funkcji y = f(x) obliczoną w punkcie x0 dla przyrostu h (który często oznacza się przez dx i nazywa różniczką argumentu funkcji y = f(x)); analogicznie dla funkcji 2 zmiennych z = f(x, y) różniczkę dz definiuje się wzorem: 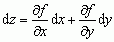 , gdzie
, gdzie 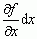 i
i 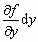 nazywają się różniczkami cząstkowymi (dz — różniczka zupełna); różniczka zupełna przybliża przyrost funkcji tym lepiej, im mniejsze są przyrosty argumentów; różniczki używa się przy szacowaniu błędów (np. w dyskusji błędów w doświadczeniach fiz.).
nazywają się różniczkami cząstkowymi (dz — różniczka zupełna); różniczka zupełna przybliża przyrost funkcji tym lepiej, im mniejsze są przyrosty argumentów; różniczki używa się przy szacowaniu błędów (np. w dyskusji błędów w doświadczeniach fiz.).