układ równań

układ równań,

mat. zbiór (skończony lub nie) równań postaci f₁(x) = g₁(x), ... , f_N(x) = g_N(x), gdzie f_i, g_i (i = 1, ... , N) są funkcjami określonymi w pewnym zbiorze A o wartościach w zbiorze B, a x = (x₁, ... , x_n) jest zbiorem niewiadomych.

W najprostszym przypadku układ 2 równań i 2 niewiadomych można zapisać ogólnie w postaci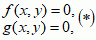

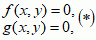
gdzie f(x, y) i g(x, y) są to pewne wyrażenia zawierające niewiadome x i y; rozwiązaniem układu równań (∗) nazywa się każdą parę liczb (x, y), która spełnia każde z równań układu (∗); rozwiązać układ równań oznacza znaleźć wszystkie jego rozwiązania. Jeżeli wyrażenia f(x, y) i g(x, y) są wielomianami (dwóch zmiennych), to układ równań nazywa się algebraicznym; układy

(A)

x² – y² = 0

x –y = 0

lub (B)

3x + 5y = 8,

x + 2y = 3

lub (C)

x² – y² = 1,

x + y = 0

są przykładami algebraicznych układów równań, przy czym układ równań (A) jest nieoznaczony (tzn. ma nieskończenie wiele rozwiązań), układ równań (B) jest oznaczony (ma dokładnie jedno rozwiązanie: x = 1, y = 1), układ równań (C) jest sprzeczny (układ nie ma rozwiązań). Do układów równań, które nie są algebraiczne, należą układy równań niewymiernych, układy równań trygonometrycznych, logarytmicznych, wykładniczych i in.; w matematyce rozważa się również układy równań różniczkowych, całkowych, wektorowych, tensorowych i inne.