równanie

równanie,

mat. wyrażenie postaci f(x) = g(x), gdzie f i g są funkcjami określonymi w pewnym zbiorze A, o wartościach w zbiorze B, a x oznacza niewiadomą lub zbiór niewiadomych.

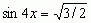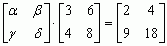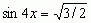W zależności od natury niewiadomych obiektów mówi się o równaniach liczbowych, np. , równaniach macierzowych, np.

,

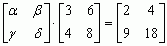równaniach funkcyjnych, np. f(x, y) = f(x) + f(y), i równaniach operatorowych. Każdy obiekt, który spełnia rozważany warunek, nazywa się rozwiązaniem równania; równanie może mieć jedno lub wiele rozwiązań (również nieskończenie wiele), może też w ogóle nie mieć rozwiązań; rozwiązać równanie oznacza znaleźć wszystkie jego rozwiązania. Równaniem o jednej niewiadomej x jest równość dwu funkcji f(x) = g(x), rozważanych we wspólnej dziedzinie; równaniem o n niewiadomych x₁, x₂, ... , x_n jest równość postaci f(x_1, x₂, ... , x_n) = g(x₁, x₂, ... , x_n). Rozważa się również układy równań, np. m równań z n niewiadomymi. Jeśli w równaniu f(x) = g(x) obie funkcje są wielomianami, to takie równanie nazywa się algebraicznym (m.in. równanie liniowe, równanie kwadratowe, równanie dwukwadratowe, równanie sześcienne, równanie diofantyczne), a jeśli któraś z funkcji jest przestępna, to równanie nazywa się przestępnym (m.in. równanie wykładnicze, logarytmiczne, trygonometryczne). W geometrii analitycznej równania interpretuje się jako określone zbiory punktów, np. równanie x² + y² = 1 przedstawia okrąg o środku w punkcie (0, 0) i promieniu 1, równanie x + y + z = 1 przedstawia płaszczyznę, równanie x² + y² + z² = 9 przedstawia sferę o promieniu 3 i środku w punkcie (0, 0, 0). Każde dwa równania, które mają ten sam zbiór rozwiązań, np. sin x = 0 oraz |cos x| = 1, są równaniami równoważnymi.