równanie kwadratowe,
mat. równanie algebraiczne postaci ax2 + bx + c = 0 (a ≠ 0);
równanie kwadratowe
Encyklopedia PWN
jeśli a, b, c są liczbami rzeczywistymi, to równanie kwadratowe ma: 1) dwa różne pierwiastki rzeczywiste, 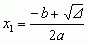 i
i  , gdy wyróżnik równania Δ = b2 − 4ac > 0; 2) jeden pierwiastek (podwójny) x = −b/2a, gdy Δ = 0; 3) dwa różne wzajemnie sprzężone pierwiastki zespolone
, gdy wyróżnik równania Δ = b2 − 4ac > 0; 2) jeden pierwiastek (podwójny) x = −b/2a, gdy Δ = 0; 3) dwa różne wzajemnie sprzężone pierwiastki zespolone 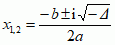 , gdy Δ < 0. Dla pierwiastków x1, x2 równania kwadratowego zachodzą następujące związki: x1 + x2 = −b/a, x1 · x2 = c/a, zwane wzorami Viète’a.
, gdy Δ < 0. Dla pierwiastków x1, x2 równania kwadratowego zachodzą następujące związki: x1 + x2 = −b/a, x1 · x2 = c/a, zwane wzorami Viète’a.
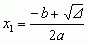 i
i  , gdy wyróżnik równania Δ = b2 − 4ac > 0; 2) jeden pierwiastek (podwójny) x = −b/2a, gdy Δ = 0; 3) dwa różne wzajemnie sprzężone pierwiastki zespolone
, gdy wyróżnik równania Δ = b2 − 4ac > 0; 2) jeden pierwiastek (podwójny) x = −b/2a, gdy Δ = 0; 3) dwa różne wzajemnie sprzężone pierwiastki zespolone 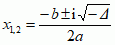 , gdy Δ < 0. Dla pierwiastków x1, x2 równania kwadratowego zachodzą następujące związki: x1 + x2 = −b/a, x1 · x2 = c/a, zwane wzorami Viète’a.
, gdy Δ < 0. Dla pierwiastków x1, x2 równania kwadratowego zachodzą następujące związki: x1 + x2 = −b/a, x1 · x2 = c/a, zwane wzorami Viète’a. 

