wyróżnik równania

wyróżnik równania,

mat. pojęcie z zakresu algebry;

wyróżnikiem równania algebraicznego φ(x) = a₀x_n + a₁x_n–1 +...+ a_n–1x + a_n = 0 (a₀ ≠ 0), mającego pierwiastki α₁, α₂, ... ,α_n nazywa się wyrażenie .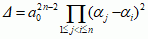

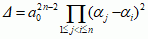Wyróżnik równania Δ równa się zeru wtedy i tylko wtedy, gdy równanie φ(x) = 0 ma co najmniej 1 pierwiastek wielokrotny. Wyróżnik równania można także wyrazić przez współczynniki wielomianu φ(x), np. wyróżnikiem równania kwadratowego (kwadratowe równanie) ax² + bx + c = 0 jest wyrażenie Δ = b² – 4ac, a równania sześciennego postaci x³ + px + q — wyrażenie Δ = –4p³ –27q².