równanie całkowe
Encyklopedia PWN
Pierwsze przykłady równań całkowych i ich rozwiązań podał 1811 J. Fourier; mianowicie dla r.c.
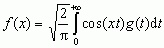
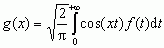
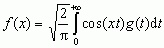
gdzie g(t) oznacza funkcję niewiadomą, a f(x) — funkcję daną, znalazł on rozwiązanie w postaci
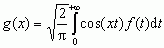
Systematyczny rozwój teorii równań całkowych rozpoczął się pod koniec XIX w., gł. dzięki pracom V. Volterry (Volterry równania całkowe) i L. Fredholma (równania całkowe Fredholma). Dalsze badania nad teorią równań całkowych rozwijały się w różnych kierunkach; jeden z nich zapoczątkował w pierwszym dziesięcioleciu XX w. D. Hilbert; dalszy rozwój tego kierunku badań, zwłaszcza w pracach T. Carlemana, F. Riesza i J. von Neumanna, doprowadził do powstania teorii operatorów w przestrzeniach Hilberta, która odgrywa obecnie ważną rolę w fizyce teoret. (gł. w mechanice kwantowej). Teoria równań całowych jest jednym z najważniejszych działów analizy mat.; wiąże się ona ściśle z zagadnieniami brzegowymi w teorii równań różniczkowych zwyczajnych i cząstkowych. Równania całkowe często występuje w zagadnieniach fizyki teoret. i techniki, np. w teorii sprężystości, w zagadnieniach rozpraszania energii promienistej, w teorii drgań, w zagadnieniach wyznaczania poziomów energ. i funkcji falowych układów kwantowych, w teorii potencjału i in.


