Volterry równania całkowe,
mat. równania całkowe (liniowe) postaci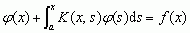 
, gdzie φ — funkcja niewiadoma, f(x) — funkcja znana, K(x, s) — funkcja znana, zw. jądrem równania całkowego;
Volterry równania całkowe
Encyklopedia PWN
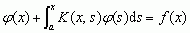, gdzie φ — funkcja niewiadoma, f(x) — funkcja znana, K(x, s) — funkcja znana, zw. jądrem równania całkowego;
gdy górna granica całkowania jest stała (x = b), to wówczas odpowiednie równanie nazywa się równaniem całkowym Fredholma, przy czym zarówno tamto, jak i to są to równania drugiego rodzaju; o równaniach całkowych pierwszego rodzaju mówi się wtedy, gdy funkcja niewiadoma występuje tylko pod znakiem całki; ponadto, gdy f(x) ≠ 0, mówi się o równaniach niejednorodnych, gdy zaś f(x) = 0 — o równaniach jednorodnych.
