równania całkowe Fredholma,
mat. w najprostszym przypadku równania całkowe postaci: 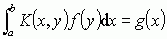 oraz f(x) − λ
oraz f(x) − λ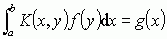 , gdzie funkcje K(x, y) (tzw. jądro równania całkowego) i g(x) są funkcjami danymi, a f oznacza funkcję niewiadomą;
, gdzie funkcje K(x, y) (tzw. jądro równania całkowego) i g(x) są funkcjami danymi, a f oznacza funkcję niewiadomą;
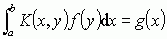 oraz f(x) − λ
oraz f(x) − λ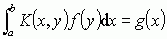 , gdzie funkcje K(x, y) (tzw. jądro równania całkowego) i g(x) są funkcjami danymi, a f oznacza funkcję niewiadomą;
, gdzie funkcje K(x, y) (tzw. jądro równania całkowego) i g(x) są funkcjami danymi, a f oznacza funkcję niewiadomą;
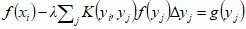 (i = 1, 2, ... , n)
(i = 1, 2, ... , n) 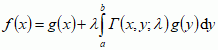 ,
, 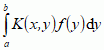 występuje operator pełnociągły (zwarty), działający w określonej przestrzeni Banacha; wyniki te rozszerzył następnie J. Schauder.
występuje operator pełnociągły (zwarty), działający w określonej przestrzeni Banacha; wyniki te rozszerzył następnie J. Schauder.